[Deeplearning] 파이토치를 이용한 딥러닝 모델 성능 개선 방법
이번엔 딥러닝 모델을 학습하면서 대표적으로 겪을 수 있는 여러 문제들을 해결해 모델의 성능을 개선하는 방법에 대해서 알아보도록 하겠습니다.
1. 과적합 개선
과적합(Overfitting)이란 학습 데이터에 대해서는 예측을 잘 하지만 테스트 데이터와 같은 학습에 사용되지 않은 데이터에 대해서 예측을 잘 못하는 현상입니다. 머신러닝 분야에서의 과적합은 항상 문제로 대두되는 만큼 지금까지 다양한 방지 기법들이 개발되었습니다. 일반적으로 모델 파라미터 수가 많으면 쉽게 나타나는 것으로 알려져 있기 때문에 과적합 현상은 모델을 깊게 만드는데 방해 요소로 작용합니다. 이때 과적합을 방지하면서 딥러닝 모델을 학습시키는 것을 정규화(Regularization) 방법이라고 합니다.
1.1 조기 종료
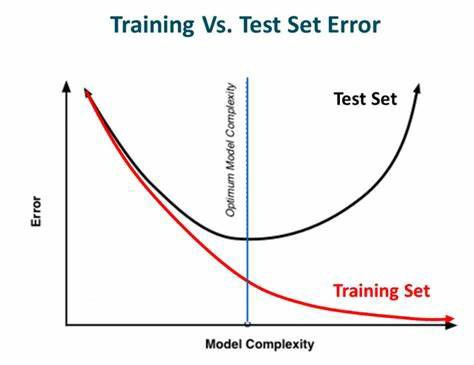
모델이 학습 데이터를 많이 공부한다면 학습 데이터에 맞춰져 모델이 최적화 될 수 있습니다. 따라서 적당한 기준을 정하여 모델 학습을 끊는 것이 조기 종료(Early stopping) 방법입니다. 아래 이미지에서와 같이 학습 반복 횟수가 많아 모델은 학습 데이터를 많이 학습하기 때문에 빨간 선과 같은 손실 함수값이 그려지고, 이때 매 에폭마다 시험 데이터의 손실 함수 값을 확인했을 때 빨간 선이 그려졌다고 가정한다면 파란색 지점에서 학습된 모델이 가장 이상적이라고 생각할 수 있습니다. 따라서 이 시점에 학습된 모델을 사용하는 것을 조기 종료라고 합니다. 또한 조기 종료는 프로그래밍 기술 보다는 아래 내용을 기억하고 있는 것이 중요합니다.
- 손실 함수값이 작다고 반드시 정확도가 높은 것은 아니다
- 학습 반복 횟수를 더 많이 할 경우 테스트 데이터의 손실 함수값이 다시 내려 오는 경우도 존재한다.
- 모델 선택에 직접적으로 시험 데이터를 사용하면 매우 위험할 수 있다. 따라서 검증 데이터를 사용해야 한다. 시험 데이터는 오직 평가 시에만 사용한다.
코드로 조기 종료 알아보기
라이브러리 불러오기
import torch
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
모델 정의하기
이전에 공부했던 ResNet 을 이용합니다. 코드가 필요하면 https://icechickentender.github.io/deeplearning/pytorch/pytorch-CNN-post/#3-resnet 을 참조하시기 바랍니다.
...생략...
resnet = modeltype('resnet18').to(device)
손실 함수 및 최적화 기법
PATH = "/content/drive/MyDrive/pytorch/models/cifar_resnet_early.pth"
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
resnet = modeltype("resnet18").to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(resnet.parameters(), lr=1e-3)
검증 데이터에 대한 손실 함수값을 연산하는 함수 정의하기
평가만 진행하기 때문에 requires_grad 를 비활성화합니다.
평가 시 정규화 기법들이 작동하지 않도록 eval 모드로 설정합니다.
함수가 끝나는 부분에 다시 모델을 학습 시켜야 하므로 train 모드로 변경합니다.
def validation_loss(dataloader):
n = len(dataloader)
running_loss = 0.0
with torch.no_grad():
resnet.eval()
for data in dataloader:
images, labels = data[0].to(device), data[1].to(device)
outputs = resnet(images)
loss = criterion(outputs, labels)
running_loss += loss.item()
resnet.train()
return running_loss / n
학습 하기
손실 함수 그래프를 그리기 위해 학습 및 검증 데이터에 대한 손실 함수값을 각각 담을 수 있는 빈 리스트를 생성합니다.
가장 낮은 검증 손실 함수값에 해당하는 모델을 저장하기 위해 손실 함수값 초기 기준을 1로 합니다.
그리고 early_stopping_loss 보다 검증 손실값이 적은 에폭이 등장한 이후에는 조기 종료를 하지 않도록 하기 위한 조건 검사 변수를 설정합니다.
train_loss_list = []
val_loss_list = []
n = len(trainloader)
early_stopping_loss = 1
early_check = True
배치 학습이 한 번 완료될 때마다 평균 손실 함수값을 저장합니다.
현재 에폭의 평가, 검증 손실 함수값을 출력합니다.
if val_loss < early_stopping_loss: 만약 현재 검증 손실값이 기준보다 작으면 모델을 저장하고 현재의 에폭, 평가, 검증 손실 함수값을 저장합니다.
학습이 완료되면 조기 종료를 한 에폭과 손실 함수값들을 출력합니다. 결과를 보면 3번째 학습 시 검증 손실 함수값이 가장 작은 것을 알 수 있습니다.
for epoch in range(51):
running_loss = 0.0
for data in trainloader:
inputs, labels = data[0].to(device), data[1].to(device)
optimizer.zero_grad()
outputs = resnet(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
train_loss = running_loss / n
train_loss_list.append(train_loss)
val_loss = validation_loss(valloader)
val_loss_list.append(val_loss)
print("[%d] train loss: %.3f, validation loss: %.3f"%(epoch+1, train_loss, val_loss))
if val_loss < early_stopping_loss and early_check:
torch.save(resnet.state_dict(), PATH)
early_stopping_train_loss = train_loss
early_stopping_val_loss = val_loss
early_stopping_epoch = epoch
early_check = False
print("Final pretrained model >> [%d] train loss: %.3f, validation loss: %.3f"
%(early_stopping_epoch+1, early_stopping_train_loss, early_stopping_val_loss))
Output :
[1] train loss: 1.434, validation loss: 1.233
[2] train loss: 0.981, validation loss: 1.024
[3] train loss: 0.768, validation loss: 0.768
... 생략 ...
Final pretrained model >> [3] train loss: 0.768, validation loss: 0.768
손실 함수값 그래프 그리기
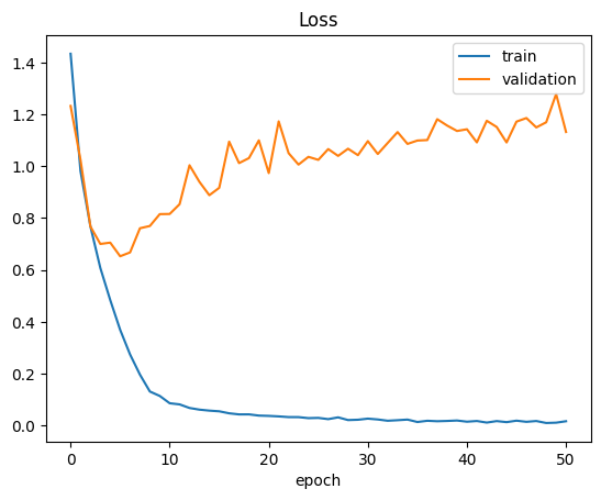
그래프를 보면 학습 손실 함수값은 학습이 진행될 수록 꾸준히 줄어들고 있지만, 검증 손실 함수값의 경우 학습이 진행된다고 해서 손실 함수값이 줄어들지 않습니다. 따라서 최초로 우리가 정한 손실 함수값 보다 적은 검증 손실 함수값이 발생한 3번째 에폭에서 학습을 중단한다면 과적합을 방지할 수 있습니다.
plt.plot(train_loss_list)
plt.plot(val_loss_list)
plt.legend(["train", "validation"])
plt.title("Loss")
plt.xlabel("epoch")
plt.show()
1.2 드롭아웃
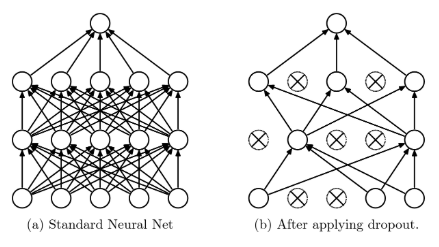
인공 신경망에서 무작위로 일정한 비율의 노드를 제외하여 학습하는 방법을 드롭아웃(Dropout)이라고 합니다. 따라서 한 번 변수 갱신이 일어날 때마다 제외된 노드와 관련 있는 변수는 갱신이 되지 않기 때문에 학습 데이터에 대한 모델 최적화를 억제할 수 있습니다. 드롭아웃의 세팅 방법에 대해서 살펴보면 출력층은 예측값이 나오는 단계이기 때문에 적용하지 않습니다. 즉, 출력층의 노드는 절대 지우지 않으며 원하는 층에만 적용할 수도 있고 제외 비율도 조정을 할 수 있습니다. 추가적으로 학습이 반복될 때마다 제외할 노드를 무작위로 선택하여 학습에서 과적합을 방지하며 시험 데이터를 이용하는 것과 같은 평가 단계에서는 드롭아웃을 적용하지 않고 원래 전체 모델을 사용합니다(.eval() 함수 선언)
nn.Dropout(0.5) 는 해당 노드에 50% 를 선택해 노드를 사용하지 않겠다는 의미로 F.relu(self.fc1(x)) 의 노드는 50개이므로 25개의 노드가 비활성화됩니다. 또다른 표현으로는 torch.nn.functional.dropout(input, p=0.5, training=True)가 있습니다.
class Regressor(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(13, 50)
self.fc2 = nn.Linear(50, 1)
self.dropout = nn.Dropout(0.5)
def forward(self, x):
x = self.dropout(F.relu(self.fc1(x)))
x = F.relu(self.fc2(x))
return x
1.3 배치 정규화
미니 배치를 이용하면 학습을 반복할 때마다 우리가 나눠 놓은 미니 배치들이 돌아가면서 사용됩니다. 학습을 한 번 할 때마다 입력값의 분포가 다르고 각 레이어의 입력값 분포 또한 다르다는 의미입니다. 기본적인 인공 신경망의 구조는 이전 층의 노드가 관련 변수들과 일차결합 연산을 거치고 그 값이 활성화 함수를 통해 다음 레이어로 가는 흐름인데, 여기서 활성화 함수로 들어가기 전에 각 노드로 들어오는 값인 피쳐값을 보정된 정규화를 통해서 항상 동일한 분포 위에 있게 합니다. 배치 정규화는 입력값들의 분포를 일정하게 하여 일반적으로 학습에 대한 수렴 속도가 빠릅니다. 또한 배치 단위의 정규화 분포는 전체의 데이터 분포와 다를 수 있기 때문에 과적합을 방지할 수 있습니다. 이 효과는 드롭아웃과 유사하며 속도가 더 빠른 것으로 알려져 있습니다. 배치 정규화는 층과 층 사이에 nn.BatchNorm2d() 를 넣어주면 됩니다.
1.4 교란 라벨
교란 라벨(DisturbLabel) 은 분류 문제에서 일정 비율만큼 라벨을 의도적으로 잘못된 라벨로 만들어서 학습을 방해하는 방법입니다. 매우 단순한 방법임에도 분류 문제에서의 과적합을 효과적으로 막을 수 있습니다.
코드로 교란 라벨 알아보기
교란 라벨 정의하기
실제 라벨을 뽑을 확률을 self.p_c로 부여하고 나머지는 self.p_i 값을 부여합니다. 예를 들면, CIFAR10 데이터를 사용한다고 가정하면, 클래스 수가 10개이고 교란 라벨 비율이 30%라면 self.p_c=73/100, self.p_i=3/100이 되고, 실제 라벨이 5라면 확률 분포는 (3/100, 3/100, 3/100, 3/100, 3/100, 73/100, 3/100, 3/100, 3/100, 3/100)이 됩니다. 여기서 6번째 가 73/100 이 되는 이유는 CIFAR10 데이터의 라벨은 0부터 9까지기 때문에 5 라벨은 6번째입니다.
만들어진 확률을 이용해 Multinoulli 분포를 통해 샘플을 뽑습니다.
10개의 원소 중 가장 큰 값의 라벨을 뽑습니다. 확률 분포를 이용해 교란 라벨을 만들기 때문에 비율이 30%라고 해서 반드시 미니 배치의 30%가 교란 라벨이 아닐 수 있습니다.
class DisturbLabel(torch.nn.Module):
"""
입력된 정답 라벨(y)을 'alpha' 값에 기반하여
일정 확률로 다른 라벨로 교란시키는 모듈
"""
def __init__(self, alpha, num_classes):
"""
Args:
alpha(float) : 라벨 교란 수준을 제어하는 파라미터
num_classes(int) : 데이터셋의 총 클래스 수
"""
super(DisturbLabel, self).__init__()
self.alpha = alpha
self.C = num_classes
# 확률 계산
# p_c: '정답' 라벨이 유지될 확률 (Probability of Correct)
# alpha 는 총 노이즈 비율이 아니라, 노이즈를 계산하는 파라미터로 사용됩니다.
# 예시 : C=10, alpha=20 (20%) 일 때
# ((C-1)/C) * (alpha/100) = (9/10) * (20/100) = 0.9 * 0.2 = 0.18
# p_c = 1 * 0.18 = 0.82
# -> 정답 라벨을 82% 확률로 유지
self.p_c = (1 - ((self.C - 1) / self.C) * (alpha / 100)) # Multinoulli distribution
# p_i: '오답' 라벨이 선택될 확률 (Probability of Incorrect)
# 'p_c'를 제외한 나머지 확률 (1-p_c)을 C-1개의 '오답' 라벨들에게 균등하게 분배합니다.
# 예시: C=10, p_c=0.82 일 때
# -> 9개의 각 오답 라벨은 2%의 확률로 선택됩니다.
# (최종 확률 분포 : 0.02, 0.02, ..., 0.82(정답), ..., 0.02) -> 합 1.0)
self.p_i = (1-self.p_c)/(self.C-1)
def forward(self, y):
"""
정답 라벨 배치(y)을 입력받아 교란된 라벨 배치를 반환합니다.
Args:
y (torch.Tensor): (Batch_size,) 형태의 정답 라벨 텐서
"""
# 1. 라벨을 scatter_ 함수에 사용하기 위해 (Batch_size, 1) 형태로 변환
y_tensor = y.type(torch.LongTensor).view(-1, 1)
depth = self.C # 클래스 수
# 2. (Batch_size, 10) 크기의 텐서를 만들고,
# '오답' 확률인 p_i(e.g., 0.02)로 모두 초기화
y_one_hot = torch.ones(y_tensor.size()[0], depth) * self.p_i
# 3. scatter_ 함수를 사용하여 '정답' 인덱스에만 '정답' 확률인 p_c (e.g., 0.82) 값을 덮어씁니다.
# dim=1: 1번 차원(클래스 차원)을 기준으로 작업
# index=y_tensor: 정답 라벨의 인덱스
# src=self.p_c: 덮어쓸 값
y_one_hot.scatter_(1, y_tensor, self.p_c)
# 4. (선택적) 원본 y의 다차원 형태를 복원하기 위한 view
# (y가 1D (Batch_size,) 였다면, (B, 10) -> (B, 10)으로 사실상 통일)
y_one_hot = y_one_hot.view(*(tuple(y.shape) + (-1,))) # create disturbed labels
# 5. Multinoulli 분포(다항 분포) 객체 생성
# 각 샘플(row)마다 [0.02, ..., 0.82, ...]와 같은 확률 분포를 가짐
distribution = torch.distributions.OneHotCategorical(y_one_hot) # sample from Multinoulli distribution
# 6. 이 분포에 따라 새로운 라벨을 '샘플링' (추출)
# 82% 확률로 정답 인덱스가, 18% 확률로 오답 인덱스가 뽑힘
# 결과: (Batch_size, 10) 크기의 `원-핫 인코딩'된 텐서
y_disturbed = distribution.sample()
# 7. 샘플링된 원-핫 텐서를 다시 클래스 인덱스(숫자)로 변환
# .max(dim=1) -> (값, 인덱스) 튜플 반환
# [1] -> 인덱스만 선택
y_disturbed = y_disturbed.max(dim=1)[1]
# 8. 최종 교란된 라벨 (Batch_size,) 텐서 반환
return y_disturbed
교란 라벨 확인하기
교란 라벨 확인을 위해 CIFAR10 데이터를 사용했습니다.
import torch
import torchvision
import torchvision.models as models
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=32, shuffle=True)
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=32, shuffle=False)
교란 라벨을 만들기 위해 정의한 DisturbLabel 객체를 선언하고, trainloader 에서 하나의 배치를 가져오고, 교란 라벨을 적용합니다. 그리고 정상적인 라벨과 교란 라벨이 적용된 라벨을 비교해보고, 교란 라벨이 적용된 비율을 출력해 봅니다.
disturblabels = DisturbLabel(alpha=30, num_classes=10)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
dataiter = iter(trainloader)
data = next(dataiter)
_, labels = data[0].to(device), data[1].to(device)
print(labels)
print()
dis_labels = disturblabels(labels).to(device)
print(dis_labels)
print()
ratio = (labels == dis_labels).float().mean()
print(ratio.item())
출력을 보면 기존 라벨에서 교란 라벨을 적용하면 라벨이 바뀐 것을 확인할 수 있으며, 비율을 보면 대략 22% 정도가 바뀐 것을 확인할 수 있습니다.
Output :
tensor([7, 8, 7, 8, 8, 6, 9, 5, 4, 9, 6, 2, 1, 2, 6, 1, 3, 6, 5, 0, 9, 6, 7, 7,
6, 4, 3, 0, 5, 5, 6, 0], device='cuda:0')
tensor([7, 8, 7, 0, 8, 6, 9, 5, 0, 9, 6, 2, 4, 2, 8, 1, 3, 6, 5, 0, 2, 6, 7, 7,
6, 4, 3, 0, 8, 1, 6, 0], device='cuda:0')
0.78125
교란 라벨을 이용해 학습해 보기
교란 라벨을 이용해 학습해 보기 위해 pytorch 에서 제공하는 resnet 모델을 사용했습니다.
resnet = models.resnet18()
resnet.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1)
num_ftrs = resnet.fc.in_features
resnet.fc = nn.Sequential(nn.Dropout2d(0.5), nn.Linear(num_ftrs, 10))
resnet = resnet.to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(resnet.parameters(), lr=1e-3)
우선 교란 라벨이 아닌 기존 라벨을 이용해 학습을 진행해 보았습니다.
# 교란 라벨을 적용하지 않고 학습
loss_1 = [] # 그래프를 그리기 위한 loss 저장용 리스트
n = len(trainloader) # 배치 개수
for epoch in range(50):
running_loss = 0.0
for data in trainloader:
inputs, labels = data[0].to(device), data[1].to(device) # 배치 데이터
optimizer.zero_grad()
outputs = resnet(inputs) # 예측값 산출
loss = criterion(outputs, labels) # 손실함수 계산
loss.backward() # 손실함수 기준으로 역전파 선언
optimizer.step() # 가중치 최적화
running_loss += loss.item()
loss_1.append(running_loss / n)
print('[%d] loss: %.3f' %(epoch + 1, running_loss / n))
print('Finished Training')
Output :
[1] loss: 1.286
[2] loss: 0.840
[3] loss: 0.660
... 생략 ...
[49] loss: 0.020
[50] loss: 0.017
Finished Training
기존 라벨을 이용한 loss 값 그래프는 다음과 같으며, 학습이 진행될 수록 loss 값이 지속적으로 감소하는 것을 확인할 수 있습니다.
plt.plot(loss_1)
plt.title("Training Loss")
plt.xlabel("epoch")
plt.show()
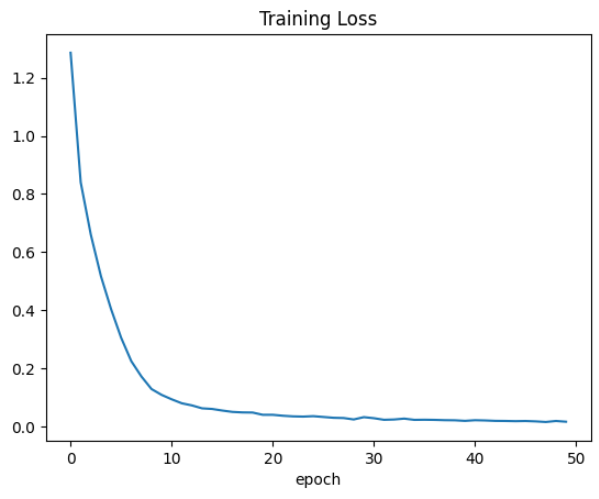
그리고 기존 라벨을 이용해 학습 시킨 모델을 테스트 데이터로 평가를 해보면 81.34% 라는 정확도를 보입니다.
correct = 0
total = 0
with torch.no_grad():
resnet.eval()
for data in testloader:
images, labels = data[0].to(device), data[1].to(device)
outputs = resnet(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Test accuracy: %.2f %%' % (100 * correct / total))
Output :
Test accuracy: 81.34 %
그럼 이제 교란 라벨을 이용해 학습을 진행해 보도록 하겠습니다. 학습 루프는 동일하지만 라벨을 교란 라벨을 사용합니다.
loss_2 = [] # 그래프를 그리기 위한 loss 저장용 리스트
n = len(trainloader) # 배치 개수
for epoch in range(50):
running_loss = 0.0
for data in trainloader:
inputs, labels = data[0].to(device), data[1].to(device) # 배치 데이터
optimizer.zero_grad()
outputs = resnet(inputs) # 예측값 산출
labels = disturblabels(labels).to(device) # 교란 라벨 사용
loss = criterion(outputs, labels) # 손실함수 계산
loss.backward() # 손실함수 기준으로 역전파 선언
optimizer.step() # 가중치 최적화
running_loss += loss.item()
loss_2.append(running_loss / n)
print('[%d] loss: %.3f' %(epoch + 1, running_loss / n))
print('Finished Training')
Output :
[1] loss: 1.330
... 생략 ...
[50] loss: 1.179
Finished Training
교란 라벨을 이용해 학습했을 때의 loss 그래프는 다음과 같습니다. 기존 라벨을 사용했을 때와는 다른 모습을 보입니다. 특정 에폭까지는 수렴하다가 그 이후에는 loss 값이 들쑥날쑥한 것을 볼 수 있습니다.
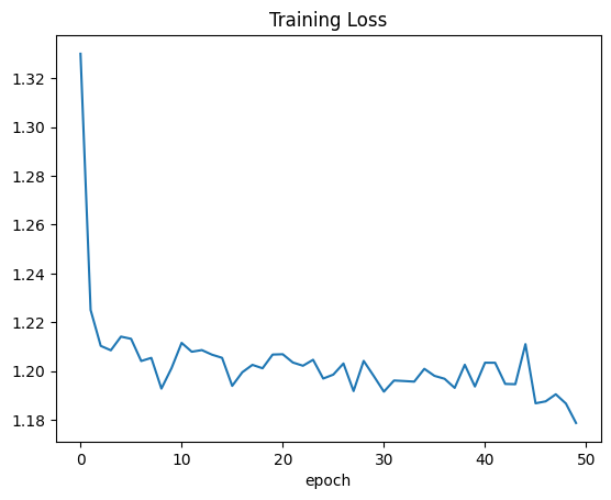
그리고 성능을 측정해 보면 82.46% 로 기존 라벨로 학습했을 때 보다 좀 더 성능이 좋은 것을 확인할 수 있습니다. 즉 앞서 배웠던 것과 같이 loss 값이 작다고 해서 무조건 학습이 잘 되는 것이 아니며, 과적합이 일어나면 지금과 같이 오히려 성능이 떨어질 수 있다는 것을 확인해 볼 수 있었습니다. 또한 이렇게 교란 라벨을 이용하면 과적합이 덜 발생해서 오히려 성능 향상이 되는 것 또한 확인할 수 있었습니다.
Output :
Test accuracy: 82.46 %
1.5 교란 값
교란 값(DisturbValue)은 회귀 문제에서 일정 비율만큼 라벨에 노이즈를 주입하여 학습 데이터에 대해 최적화를 방해하는 방법입니다. 매우 간단하며 어떠한 모델에도 적용할 수 있다는 것이 가장 큰 장점입니다.
코드로 교란 값 알아보기
노이즈 생성하기
데이터는 이전에 회귀 모델을 알아보기 위해 사용했던 집값 데이터를 사용하였습니다.
df = pd.read_csv("/content/drive/MyDrive/pytorch/data/reg.csv", index_col=[0])
# 데이터를 넘파이 배열로 만들기
X = df.drop('Price', axis=1).to_numpy() # 데이터프레임에서 타겟값(Price)을 제외하고 넘파이 배열로 만들기
Y = df['Price'].to_numpy().reshape((-1,1)) # 데이터프레임 형태의 타겟값을 넘파이 배열로 만들기
임의로 정한 정규분포에 따른 노이즈를 생성합니다.
노이즈 타깃이 아닌 값은 노이즈를 0으로 합니다.
def noise_generator(x, alpha):
noise = torch.normal(0, 1e-8, size=(len(x), 1))
noise[torch.randint(0, len(x), (int(len(x)*(1-alpha)),))] = 0
return noise
dataiter = iter(trainloader)
data = next(dataiter)
labels = data[1]
print(labels)
print()
disturb_labels = labels + noise_generator(labels, 0.3)
print(disturb_labels)
Output :
tensor([[0.8667],
[0.0000],
[0.3400],
[0.2267],
[0.6978],
[0.1956],
[0.1022],
[0.3689],
[1.0000],
[0.3889],
[0.1889],
[0.3644],
[0.5933],
[0.1844],
[0.3556],
[0.3356],
[0.4067],
[0.3956],
[0.6311],
[0.3867],
[0.0444],
[0.4111],
[0.2378],
[1.0000],
[0.2556],
[0.3667],
[0.3089],
[0.4200],
[0.3956],
[0.3089],
[1.0000],
[0.4444]])
tensor([[ 8.6667e-01],
[-1.0853e-08],
[ 3.4000e-01],
[ 2.2667e-01],
[ 6.9778e-01],
[ 1.9556e-01],
[ 1.0222e-01],
[ 3.6889e-01],
[ 1.0000e+00],
[ 3.8889e-01],
[ 1.8889e-01],
[ 3.6444e-01],
[ 5.9333e-01],
[ 1.8444e-01],
[ 3.5556e-01],
[ 3.3556e-01],
[ 4.0667e-01],
[ 3.9556e-01],
[ 6.3111e-01],
[ 3.8667e-01],
[ 4.4444e-02],
[ 4.1111e-01],
[ 2.3778e-01],
[ 1.0000e+00],
[ 2.5556e-01],
[ 3.6667e-01],
[ 3.0889e-01],
[ 4.2000e-01],
[ 3.9556e-01],
[ 3.0889e-01],
[ 1.0000e+00],
[ 4.4444e-01]])
교란 값을 이용해 학습하기
모델은 기본적인 회귀 모델을 사용하였습니다.
model = Regressor()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-7)
기존 데이터를 사용하여 학습을 진행하면 다음과 같습니다.
loss_1 = [] # 그래프를 그리기 위한 loss 저장용 리스트
n = len(trainloader)
for epoch in range(400): # 400번 학습을 진행한다.
running_loss = 0.0
for data in trainloader: # 무작위로 섞인 32개 데이터가 있는 배치가 하나 씩 들어온다.
inputs, values = data # data에는 X, Y가 들어있다.
optimizer.zero_grad() # 최적화 초기화
outputs = model(inputs) # 모델에 입력값 대입 후 예측값 산출
loss = criterion(outputs, values) # 손실 함수 계산
loss.backward() # 손실 함수 기준으로 역전파 설정
optimizer.step() # 역전파를 진행하고 가중치 업데이트
running_loss += loss.item() # epoch 마다 평균 loss를 계산하기 위해 배치 loss를 더한다.
loss_1.append(running_loss/n) # MSE(Mean Squared Error) 계산
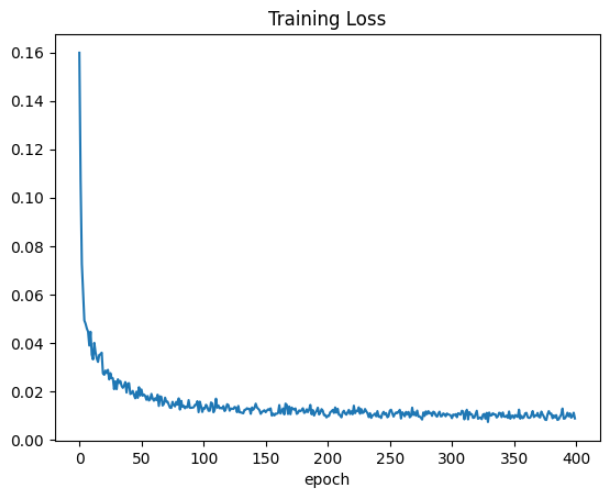
기존 데이터로 학습했을 때의 손실값 그래프 출력하면 학습이 진행될 수록 loss 값이 줄어들게 수렴하는 것을 확인할 수 있습니다.
plt.plot(loss_1)
plt.title("Training Loss")
plt.xlabel("epoch")
plt.show()
교란 값을 이용해 학습 진행
loss_2 = [] # 그래프를 그리기 위한 loss 저장용 리스트
n = len(trainloader)
for epoch in range(400): # 400번 학습을 진행한다.
running_loss = 0.0
for data in trainloader: # 무작위로 섞인 32개 데이터가 있는 배치가 하나 씩 들어온다.
inputs, values = data # data에는 X, Y가 들어있다.
optimizer.zero_grad() # 최적화 초기화
values = values + noise_generator(values, 0.3) # label 에 교란 값 추가
outputs = model(inputs) # 모델에 입력값 대입 후 예측값 산출
loss = criterion(outputs, values) # 손실 함수 계산
loss.backward() # 손실 함수 기준으로 역전파 설정
optimizer.step() # 역전파를 진행하고 가중치 업데이트
running_loss += loss.item() # epoch 마다 평균 loss를 계산하기 위해 배치 loss를 더한다.
loss_2.append(running_loss/n) # MSE(Mean Squared Error) 계산
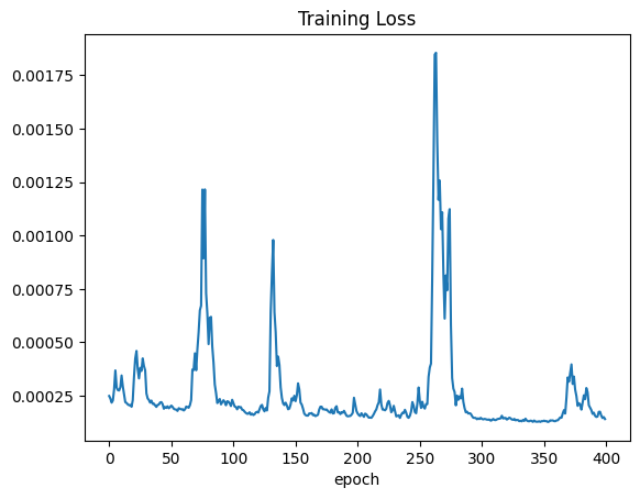
교란 값을 이용해 학습을 진행했을 때의 손실값 그래프 출력하면 기존 데이터와는 다르게 loss 값이 꾸준히 수렴하는 것이 아니라 들쑥날쑥 한 것을 확인할 수 있습니다.
1.6 라벨 스무딩
분류 문제에서 원-핫 벡터를 생각해 보면 (1,0,0)과 같이 0과 1로 구성되어 있고 우리는 소프트맥스나 시그모이드 함수를 통해 0과 1 사이의 예측값을 출력합니다. 이때 교차 엔트로피 손실 함수를 계산할 때 실제 값을 0과 1이 아닌, 예를 들어 0.1과 0.8로 구성해서 과적합을 방지하는 기술이 라벨 스무딩(Label Smoothing)입니다. 직관적으로 말하자면 0과 1을 맞춰야 하는 문제에서 예측값이 0.7이 나왔다면 원래 1을 맞추기 위해 1에 가까워지도록 학습이 될 것입니다. 이때 기준을 0.8로 낮추면서 0.7만 나와도 이 정도면 맞았다고 모델이 스스로를 인정하면서 실제값에 가깝게 가려고 하지 않고 정답을 맞히게 되어 과적합을 막아주는 개념입니다. 라벨 스무딩의 공식은 다음과 같습니다.
\[y_{ls} = (1-\alpha)y+\frac{\alpha}{K-1}(1-y)\]- K 는 클래스 수
- $\alpha$ 는 스무딩 비율,
- $y$는 0또는 1 (0은 라벨 0을 의미하며, 1은 라벨 1을 의미함)
예제와 위 공식을 이용해 실제 라벨 스무딩을 적용해 보면 클래스가 3개인 분류 문제에서는 라벨값이 0, 1, 2이고 원 핫 벡터로 표현할 때에는 (1,0,0), (0,1,0), (0,0,1)이 됩니다. 이때, 스무딩 비율이 0.1이면 위 공식에 의해 모든 실제 타깃에서 1은 0.9으로 0은 0.05으로 변환하여 0과 1 사이의 차이를 0.9과 0.05 으로 줄입니다.
파이토치에서 제공하는 크로스 엔트로피 함수 nn.CrossEntropyLoss()는 실제 라벨의 원 핫 벡터를 입력으로 받을 수 없습니다. 따라서 라벨 스무딩을 적용할 경우 원 핫 벡터를 사용할 수 있도록 별도로 손실 함수를 만들어 주어야 합니다.
코드로 알아보는 라벨 스무딩
만약 CIFAR10 데이터를 이용하는 경우, 클래스는 10개로 지정하고 적절한 스무딩 비율을 넣어 nn.CrossEntropyLoss() 대신 LabelSmoothingLoss 로 criterion 을 선언합니다.
class LabelSmoothingLoss(nn.Module):
def __init__(self, classes, smoothing=0.0, dim=-1):
super(LabelSmoothingLoss, self).__init__()
self.confidence =1.0 - smoothing
self.smoothing = smoothing
self.cls = classes
self.dim = dim
def forward(self, pred, target):
pred = pred.log_softmax(dim=self.dim)
with torch.no_grad():
true_dist = torch.zeros_like(pred)
true_dist.fill_(self.smoothing / (self.cls-1))
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
return torch.mean(torch.sum(-true_dist * pred, dim=self.dim))
2. 데이터 불균형
데이터 불균형(Data imbalance)이란 데이터 세트 내의 클래스의 분포가 불균형한 것을 의미합니다. 불균형은 특정 클래스에 과적합을 야기할 수 있습니다. 이러한 데이터 불균형을 해결하는 방법에 대해서 살펴보도록 하겠습니다.
2.1 가중 무작위 샘플링
주어진 데이터가 불균형 데이터라도 우리는 미니 배치를 균형 데이터로 뽑을 수 있습니다. 즉 배치를 만들 때마다 각 클래스를 동일한 개수를 뽑는다면 한 번 학습 시 균형 데이터를 사용하게 되는 것입니다. 이 방법을 가중 무작위 샘플링(Weighted random sampling)이라고 합니다.
코드로 가중 무작위 샘플링 알아보기
라이브러리 임포트
import torch
from torch.utils.data import DataLoader
import torchvision
import numpy as np
import torchvision.transforms as tr
가중치 함수 만들기
우선 우리가 사용할 데이터는 클래스의 수가 2개이고, (14개, 4개) 로 되어 있는 이미지 데이터를 사용합니다. 즉 클래스가 0인 것이 14개, 클래스가 1인 것이 4개가 있다고 생각하시면 됩니다.
데이터를 기준으로 코드 설명을 하자면, 각 클래스마다 라벨의 개수를 세어줍니다. 그리고 라벨이 뽑힐 가중치를 만들어주어야 하는데 우리가 원하는 것은 각 클래스별로 라벨을 균등하게 뽑고 싶은 상황입니다. 그렇다면 개수가 적은 데이터에는 높은 확률을 개수가 많은 데이터에는 낮은 확률을 부여하도록 해야 합니다. 그래서 가중치로 1/(각 라벨의 개수) 그래서 1/count 로 동일하게 해당 라벨 전체에 할당합니다. 이렇게 하면 라벨이 많은 클래스일 수록 더 적은 확률 값을 가지게 됩니다.
그리고 weight_list 에는 라벨의 개수 만큼 가중치 값을 넣어줍니다.
def make_weights(labels, nclasses):
"""
Args:
labels : 라벨 데이터
nclasses : 클래스의 수
"""
# 라벨이 담긴 자료구조를 numpy array 로 변경
labels = np.array(labels)
weight_list = [] # 클래스별 가중치를 담을 리스트 선언
for cls in range(nclasses):
idx = np.where(labels == cls)[0]
count = len(idx)
weight = 1/count # 1/라벨의 개수 확률
weights = [weight] * count # 확률x라벨 개수 만큼 가지는 weights 리스트를 정의
weight_list += weights # weight_list 에 weights 를 추가
return weight_list
이미지 데이터 불러오기
위에서 언급한 것과 같이 이번 예시에서는 사진을 보고 호랑이인지 사자인지 구분하는 이미지를 사용할 것이며 사자 데이터가 4개, 호랑이 데이터가 14개 분포되어 있습니다.
transf = tr.Compose([tr.Resize((16, 16)), tr.ToTensor()])
trainset = torchvision.datasets.ImageFolder(root="/content/drive/MyDrive/pytorch/data/class", transform=transf)
가중치 생성하기
가중치를 생성한 후 텐서로 변환합니다.
weights = make_weights(trainset.targets, len(trainset.classes))
weights = torch.DoubleTensor(weights)
print(weights)
가중치 텐서를 보면 모든 데이터에 대한 각각의 가중치가 있음을 알 수 있습니다. 또한 각 클래스의 가중치의 합이 1로 같습니다. 즉 하나의 클래스를 뽑을 확률이 같다는 의미입니다.
Output :
tensor([0.2500, 0.2500, 0.2500, 0.2500, 0.0714, 0.0714, 0.0714, 0.0714, 0.0714,
0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.0714, 0.0714],
dtype=torch.float64)
데이터로더 생성하기
sampler = torch.utils.data.sampler.WeightedRandomSampler(weights, len(weights))
trainloader_wrs = DataLoader(trainset, batch_size=6, sampler=sampler)
trainloader_rs = DataLoader(trainset, batch_size=6, shuffle=True)
가중 무작위 샘플링 vs 무작위 샘플링
배치 사이즈를 6개로 한 경우 2개의 클래스가 각각 3개로 들어오는 것이 이상적일 것입니다. 하지만 확률적으로 데이터를 뽑기 때문에 반드시 3개씩 뽑히지 않을 수 있지만, 무작위 샘플링 보다는 가중 무작위 샘플링이 좀 더 균형 잡힌 데이터가 만들어지는 것을 확인할 수 있습니다.
for epoch in range(3):
for data in trainloader_wrs:
print(data[1])
Output :
tensor([1, 0, 0, 1, 0, 0])
tensor([0, 0, 1, 1, 0, 1])
tensor([1, 0, 1, 1, 0, 0])
tensor([0, 1, 0, 1, 0, 1])
tensor([0, 1, 0, 0, 0, 0])
tensor([1, 0, 0, 0, 0, 0])
tensor([0, 0, 0, 1, 1, 0])
tensor([1, 1, 1, 1, 0, 1])
tensor([0, 1, 0, 0, 0, 1])
for epoch in range(3):
for data in trainloader_rs:
print(data[1])
Output :
tensor([1, 1, 1, 1, 1, 1])
tensor([1, 1, 1, 1, 1, 0])
tensor([0, 1, 1, 0, 1, 0])
tensor([1, 1, 0, 1, 1, 1])
tensor([1, 1, 1, 0, 1, 1])
tensor([1, 0, 1, 1, 0, 1])
tensor([0, 0, 1, 1, 1, 1])
tensor([1, 1, 1, 1, 1, 1])
tensor([0, 0, 1, 1, 1, 1])
2.2 가중 손실 함수
파이토치의 nn.CrossEntropyLoss 는 가중 손실 함수를 제공합니다. 따라서 미리 정의된 weight 를 입력하면 쉽게 구현이 가능합니다.
예를 들어 10개의 클래스 별 이미지 개수를 알고 있다고 하면, 가중 손실 함수는 데이터가 적은 클래스에 대해서 큰 가중치를 부여함으로써 업데이트 균형을 맞추려는 의도를 가지고 있습니다.
이 예시는 각 클래스의 확률 x/sum(num_ins) 을 구한 뒤 1에서 뺀 값을 가중치로 사용합니다. 그 다음 텐서로 변환된 가중치를 nn.CrossEntroypyLoss 에 넣어줍니다.
import torch.nn as nn
import torch
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
num_ins = [40, 45, 30, 62, 70, 153, 395, 46, 75, 194]
weights = [1-(x/sum(num_ins)) for x in num_ins]
class_weights = torch.FloatTensor(weights).to(device)
criterion = nn.CrossEntropyLoss(weight=class_weight)
2.3 혼동 행렬
혼동 행렬(Confusion matrix)은 데이터 불균형의 직접적인 해결책은 될 수 없지만 결과를 행렬화하여 각 클래스의 분포와 정확도를 확인하여 불균형 데이터로 예측 쏠림 현상을 인지할 수 있으며, 다양한 결과 해석에서 사용됩니다. 혼동 행렬에 대해서는 나중에 따로 포스트로 다뤄보도록 하겠습니다.
from sklearn.metrics import confusion_matrix
import seaborn as sns
from matplotlib import pyplot as plt
actual = [1,1,1,0,0,0,0,0,2,2,2,2,2,2,2,2]
prediction = [1,2,2,0,2,2,1,2,0,1,0,2,2,2,2,2]
c_mat = confusion_matrix(actual, prediction) # 실제 라벨, 예측값
plt.figure(figsize = (8,6))
sns.heatmap(c_mat, annot=True, fmt="d", cmap='Blues',linewidths=.5)
b, t = plt.ylim()
b += 0.5
t -= 0.5
plt.ylim(b, t)
plt.savefig('confusion_matrix.png')
plt.show()
3. 준지도 학습
지도 학습이 정답이 있는 데이터를 사용하여 모델을 학습했다면, 준지도 학습(Semi-supervised learning)은 정답이 있는 데이터와 정답이 없는 데이터를 함께 사용하여 모델을 학습시키는 방법으로써 더 많은 데이터를 확보하여 성능 향상에 도움을 줄 수 있습니다.
3.1 의사 라벨링
의사 라벨링(Pseudo labeling)은 준지도 학습 중 가장 기본적으로 사용되는 방법입니다. 우리가 라벨이 없는 데이터를 지도 학습에 사용하려면 라벨을 달아 주어야 합니다. 따라서 이미 학습된 모델을 이용하여 라벨링이 되지 않은 데이터를 예측한 후, 그 예측값을 기준으로 라벨링을 하여 기존의 학습 데이터와 함께 학습에 사용하는 방법이 의사 라벨링입니다. 여기서 주의할 점은 예측값을 라벨로 이용하기 때문에 라벨에 대한 불확실성이 존재합니다. 따라서 무분별한 사용은 자제해야 하며, 다양한 형태로 모델을 구현할 수 있습니다. 우리는 2가지 의사 라벨링 방법을 정의하여 성능 향상을 달성합니다.
코드로 의사 라벨링 알아보기
라이브러리 불러오기
import torch
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader, Dataset
import numpy as np
import torch.optim as optim
from tqdm import tqdm
import torch.nn as nn
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
데이터 세트 정의하기
class MyDataset(Dataset):
def __init__(self, x_data, y_data, transform=None):
self.x_data = x_data
self.y_data = y_data
self.transform = transform
self.len = len(y_data)
def __getitem__(self, index):
sample = self.x_data[index], self.y_data[index]
if self.transform:
sample = self.transform(sample)
return sample
def __len__(self):
return self.len
데이터 전처리 정의하기
class TrainTransform:
def __call__(self, sample):
inputs, labels = sample
transf = transforms.Compose([transforms.ToPILImage(),
transforms.RandomHorizontalFlip(),
transforms.ToTensor()])
final_output = transf(inputs)
return final_output, labels
데이터 세트 나누기
실험을 위해 데이터 세트를 두 개의 데이터 세트로 나누는 함수를 정의합니다.
def balanced_subset(data, labels, num_cls, num_data):
"""
전체 데이터셋(data, labels)을 두 개의 서브셋으로 분리합니다.
1. (data1, labels1): 'num_data' 개수만큼 클래스별로 균등하게 추출된 '균형 서브셋(balanced subset)
2. (data2, labels2): 1번에 포함되지 않은 나머지 데이터
MNIST 예시 기준
data : 전체 MNIST 이미지 텐서
labels : 전체 MNIST 라벨 텐서
num_cls : 10
num_data : 2000(추출할 총 데이터 개수)
"""
# 1. 서브셋1(data1)에 클래스별로 몇 개씩 할당할지 계산
# num_data_per_classes = 2000 // 10 = 200
# 즉, 각 클래스마다 200개씩 추출합니다.
num_data_per_class = num_data // num_cls
# 2. 결과를 저장할 빈 텐서 초기화
data1 = torch.tensor([], dtype=torch.float)
data2 = torch.tensor([], dtype=torch.float)
labels1 = torch.tensor([], dtype=torch.long)
labels2 = torch.tensor([], dtype=torch.long)
# 3. 클래스별로 반복
for cls in range(num_cls):
# 현재 클래스에 해당하는 모든 데이터의 인덱스(위치)를 찾음
# (e.g., cls=7 일 때, 전체 라벨 중 '7인' 것들의 인덱스 [5, 12, 29, ...])
idx = np.where(labels.numpy() == cls)[0]
# 찾은 인덱스들을 무작위로 섞음
# (e.g., [5, 12, 29, ...] -> [29, 5, 12, ...])
# replace=False: 비복원 추츨 (중복 없이 섞기)
shuffled_idx = np.random.choice(len(idx), len(idx), replace=False)
# 셔플된 인덱스를 사용해 data1 / data2 분리
# 셔플된 인덱스에서 앞에서부터 200개를 선택
# 해당 인덱스의 이미지와 라벨을 data1, labels1 에 추가
# 셔플된 인덱스에서 200개 이후의 나머지 인덱스 전체를 선택
# 해당 인덱스의 이미지와 라벨을 data2, labels2 에 추가
data1 = torch.cat([data1, data[shuffled_idx[:num_data_per_class]]], dim=0)
data2 = torch.cat([data2, data[shuffled_idx[num_data_per_class:]]], dim=0)
labels1 = torch.cat([labels1, labels[shuffled_idx[:num_data_per_class]]], dim=0)
labels2 = torch.cat([labels2, labels[shuffled_idx[num_data_per_class:]]], dim=0)
return data1, data2, labels1, labels2
데이터 불러오기
숫자 판별 데이터인 MNIST 데이터를 불러옵니다.
전체 데이터 수는 60,000 개로 이 중 2000 개를 학습 및 검증 데이터로 사용하며, 학습 데이터와 검증 데이터도 1000개 로 나누어 사용합니다. 나머지 58,000개 데이터는 unlabeled 데이터로 사용합니다.
trainset = torchvision.datasets.MNIST(root="./data", train=True, download=True)
labeled_data, unlabeled_data, labels, unlabels = balanced_subset(trainset.data,
trainset.targets, num_cls=10, num_data=2000)
train_images, val_images, train_labels, val_labels = balanced_subset(labeled_data, labels,
num_cls=10, num_data=1000)
데이터로더 정의하기
train_images = train_images.unsqueeze(1)
val_images = val_images.unsqueeze(1)
trainset = MyDataset(train_images, train_labels, transform=TrainTransform())
trainloader = DataLoader(trainset, batch_size=128, shuffle=True)
validationset = MyDataset(val_images, val_labels)
valloader = torch.utils.data.DataLoader(validationset, batch_size=128, shuffle=False)
unlabeled_images = unlabeled_data.unsqueeze(1)
unlabeledset = MyDataset(unlabeled_images, unlabels)
unlabeledloader = DataLoader(unlabeledset, batch_size=256, shuffle=True)
평가 데이터를 불러옵니다.
transform = transforms.Compose([transforms.ToTensor()])
testset = torchvision.datasets.MNIST(root="./data", train=False, download=True,
transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False)
모델 정의하기
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(1, 64, 3), nn.ReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(64, 192, 3, padding=1), nn.ReLU(),
nn.MaxPool2d(2, 2))
self.classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(192*6*6, 1024), nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(1024, 512), nn.ReLU(),
nn.Linear(512, 10))
def forward(self, x):
x = self.features(x)
x = x.view(-1, 192*6*6)
x = self.classifier(x)
return x
model = Net().to(device)
손실 함수 및 최적화 기법 정의하기
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
정확도 평가 함수 정의하기
def accuracy(dataloader):
correct = 0
total = 0
with torch.no_grad():
model.eval()
for data in dataloader:
images, labels = data[0].to(device), data[1].to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
acc = 100*correct/total
model.train()
return acc
지도 학습 수행하기
검증 정확도를 계산하여 가장 높은 검증 정확도를 기준으로 모델 파라미터를 저장합니다.
best_acc = 0
for epoch in range(501):
correct = 0
total = 0
for traindata in trainloader:
inputs, labels = traindata[0].to(device), traindata[1].to(device)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
_, predicted = torch.max(outputs.detach(), 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
val_acc = accuracy(valloader)
if val_acc >= best_acc:
best_acc = val_acc
torch.save(model.state_dict(), "/content/drive/MyDrive/pytorch/models/cifar_model_for_pseudo_baseline.pth")
print("[%d] train acc: %.2f, validation acc: %.2f-Saved the best model" %(epoch, 100*correct/total, val_acc))
elif epoch %10 == 0:
print("[%d] train acc: %.2f, validation acc: %.2f" %(epoch, 100*correct/total, val_acc))
Output :
[0] train acc: 99.90, validation acc: 70.60-Saved the best model
[10] train acc: 99.70, validation acc: 53.00
[18] train acc: 99.20, validation acc: 72.60-Saved the best model
[20] train acc: 99.90, validation acc: 55.00
... 생략 ...
[490] train acc: 100.00, validation acc: 47.00
[500] train acc: 99.80, validation acc: 53.20
지도 학습 성능 평가하기
지도 학습을 진행했을 때는 성능이 69.65% 를 얻을 수 있었습니다.
model.load_state_dict(torch.load("/content/drive/MyDrive/pytorch/models/cifar_model_for_pseudo_baseline.pth"))
accuracy(testloader)
Output :
69.65
준지도 학습1을 위한 모델을 재정의하기
model = Net().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
준지도 학습1 수행하기
의사 라벨링은 정확한 라벨과 부정확한 라벨이 섞여있습니다. 따라서 훈련 데이터와 동일하게 모델 최적화에 사용하게 된다면 오히려 좋지 않은 결과를 초래할 수 있습니다. 따라서 훈련 라벨과 의사 라벨을 구분하여 따로 손실 함수(L_t 와 L_p) 를 계산한 뒤 둘을 더해 전체 손실 함수L(L=L_t + alpha*L_p)을 정의합니다. 이때 의사 라벨을 이용하는 손실 함수 부분에 가중치 alpha 를 주어 학습 개입을 조절할 수 있습니다. 즉, alpha=0 이면 학습 데이터로만 모델을 최적화한다는 의미이고, alpha 가 커질수록 의사 라벨의 영향도가 커진다는 의미입니다. 따라서 연구마다 영향도의 차이가 다를 수 있으니 적절한 alpha 를 정의하는 것이 중요합니다.
이 예시에서는 처음 epoch 100번까지는 alpha=0으로 학습을 진행하고 이후 epoch 이 450이 될 때까지 일정하게 alpha 를 높여 학습을 시행합니다. 450회가 지나면 alpha 를 alpah_t로 고정하여 학습을 진행하여 마무리합니다. alpha 를 0부터 1e-4까지 점차 높여 학습을 진행하는 것입니다.
alpha = 0
alpha_t = 1e-4
T1 = 100
T2 = 450
best_acc = 0
학습 루프는 지도 학습과 동일하며, 위에서 설명한 것과 같이 의사 라벨 데이터를 이용한 손실 함수값을 특정 에폭에 따라 학습 데이터의 손실 함수값에 특정 비율로 합하도록하는 부분만 추가를 했습니다.
사용하는 의사 라벨 데이터에는 라벨이 따로 없으며, alpha 값이 0보다 클 경우 모델의 출력 벡터에서 가장 큰 값을 1로하고 나머지 값을 0으로 하여 10개의 값 중에 가장 큰 값을 가지는 것을 클래스로 보는 방법을 사용합니다. 즉 poutputs 의 shape 는 [256, 10] 이고, torch.max 를 적용하면 10개의 값들 중에서 가장 큰 값을 가지는 것을 클래스로 보는 것입니다. 256 은 배치 사이즈이며, 10은 클래스의 개수입니다. 그래서 이렇게 만든 plabels 를 의사 라벨로 사용합니다.
for epoch in range(501):
correct = 0
total = 0
for traindata, pseudodata in zip(trainloader, unlabeledloader):
inputs, labels = traindata[0].to(device), traindata[1].to(device)
pinputs = pseudodata[0].to(device)
optimizer.zero_grad()
outputs = model(inputs)
if alpha > 0:
poutputs = model(pinputs)
_, plabels = torch.max(poutputs.detach(), 1)
loss = criterion(outputs, labels) + alpha*criterion(poutputs, plabels)
else:
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
_, predicted = torch.max(outputs.detach(), 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
if (epoch > T1) and (epoch < T2):
alpha = alpha_t * (epoch-T1)/(T2-T1)
elif epoch >= T2:
alpha = alpha_t
val_acc = accuracy(valloader)
if val_acc >= best_acc:
best_acc = val_acc
torch.save(model.state_dict(), "/content/drive/MyDrive/pytorch/models/cifar_model_for_pseudo_label.pth")
print("[%d] train acc: %.2f, validation acc: %.2f -Saved the best model" %(epoch, 100*correct/total, val_acc))
elif epoch %10 == 0:
print("[%d] train acc: %.2f, validation acc: %.2f" %(epoch, 100*correct/total, val_acc))
Output :
[0] train acc: 91.41, validation acc: 76.20 -Saved the best model
[0] train acc: 91.41, validation acc: 73.60
[0] train acc: 92.45, validation acc: 65.90
... 생략 ...
[500] train acc: 99.67, validation acc: 79.60
[500] train acc: 99.60, validation acc: 80.10
준지도 학습1 성능 평가하기
평가 정확도는 79.52% 로 무려 대략 10% 가량의 성능 향상을 확인할 수 있었습니다.
model.load_state_dict(torch.load("/content/drive/MyDrive/pytorch/models/cifar_model_for_pseudo_label.pth"))
accuracy(testloader)
Output :
79.52
준지도 학습2을 위한 모델을 재정의하기
이번 방법에서는 학습 데이터로 학습된 사전 훈련 모델을 가지고 와서 의사 라벨을 생성한 뒤 이를 실제 라벨처럼 사용해 봅니다.
model = Net().to(device)
model.load_state_dict(torch.load("/content/drive/MyDrive/pytorch/models/cifar_model_for_pseudo_baseline.pth"))
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
의사 라벨 생성하기
사전 학습 모델로 예측된 출력 벡터의 가장 큰 원소가 0.99가 넘으면 의사 라벨로 사용합니다.
pseudo_threshold = 0.99
pseudo_images = torch.tensor([], dtype=torch.float)
pseudo_labels = torch.tensor([], dtype=torch.long)
with torch.no_grad():
for data in tqdm(unlabeledloader):
model.eval()
images = data[0].to(device)
outputs = model(images)
outputs = torch.nn.functional.softmax(outputs, dim=1)
max_val, predicted = torch.max(outputs.detach(), 1)
idx = np.where(max_val.cpu().numpy() >= pseudo_threshold)[0]
if len(idx) > 0:
pseudo_images = torch.cat((pseudo_images, images.cpu()[idx]), 0)
pseudo_labels = torch.cat((pseudo_labels, predicted.cpu()[idx]), 0)
준지도 학습2를 위한 데이터로더 정의하기
pseudo_dataset = MyDataset(pseudo_images, pseudo_labels)
pseudoloader = DataLoader(pseudo_dataset, batch_size=256, shuffle=True)
준지도 학습2 수행하기
우선 모델 초기화를 진행해 줍니다.
model = Net().to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
alpha = 0
alpha_t = 1e-4
T1 = 20
T2 = 450
best_acc = 0
for epoch in range(501):
correct = 0
total = 0
for traindata, pseudodata in zip(trainloader, pseudoloader):
inputs, labels = traindata[0].to(device), traindata[1].to(device)
pinputs, plabels = pseudodata[0].to(device), pseudodata[1].to(device)
optimizer.zero_grad()
outputs = model(inputs)
poutputs = model(pinputs)
loss = criterion(outputs, labels) + alpha*criterion(poutputs, plabels)
loss.backward()
optimizer.step()
_, predicted = torch.max(outputs.detach(), 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
if (epoch > T1) and (epoch < T2):
alpha = alpha_t*(epoch-T1)/(T2-T1)
elif epoch >= T2:
alpha = alpha_t
val_acc = accuracy(valloader)
if val_acc >= best_acc:
best_acc = val_acc
torch.save(model.state_dict(), "/content/drive/MyDrive/pytorch/models/cifar_model_for_pseudo_label2.pth")
print("[%d] train acc:%.2f, validation acc:%.2f - Saved the best model" %(epoch, 100*correct/total, val_acc))
elif epoch % 10 == 0:
print("[%d] train acc : %.2f, validation acc: %.2f" %(epoch, 100*correct/total, val_acc))
Output :
[0] train acc:17.90, validation acc:52.70 - Saved the best model
[1] train acc:42.20, validation acc:54.80 - Saved the best model
[2] train acc:47.50, validation acc:56.10 - Saved the best model
[5] train acc:75.60, validation acc:58.30 - Saved the best model
... 생략 ...
[490] train acc : 100.00, validation acc: 19.10
[500] train acc : 100.00, validation acc: 15.30
준지도 학습2 성능 평가하기
준지도 학습1과 달리 학습 중인 모델이 아닌 학습 데이터로 학습한 모델과 threshold 를 이용해 학습 전에 의사 레벨을 달아보았습니다. 성능은 78.48% 학습 데이터만 사용한 baseline 모델보다 대략 9%나 좋은 성능을 확인할 수 있었습니다.
model.load_state_dict(torch.load("/content/drive/MyDrive/pytorch/models/cifar_model_for_pseudo_label2.pth"))
accuracy(testloader)
Output :
78.48
마치며
이번 파이토치를 이용한 딥러닝 성능 개선 포스트를 마지막으로 파이토치 기본 다지기 공부를 마쳤습니다. 이번 성능 개선에서는 이론에서만 알고 있던 딥러닝 모델 성능 개선과 관련된 것들을 실전으로 직접 해볼 수 있어 실전 경험을 많이 쌓을 수 있었습니다. 그리고 이번 성능 개선 포스트를 마지막으로 이제 파이토치 기본 다지기 포스트 정리가 끝날 예정입니다. 이전 포스트에서도 언급을 했지만 저는 딥러닝호형 저 딥러닝을 위한 파이토치 입문 이라는 책을 참고하여 포스트를 작성하였습니다. 이 책은 파이토치 입문에 대한 책이지만 이론적인 부분 특히 수식 그리고 코드 설명에 대해서는 설명이 조금 부족합니다만, 책에서 제공되는 파이토치 코드는 실제 딥러닝 모델을 구현하고, 학습하는 루프까지 잘 정리가 되어 있어 저처럼 이전에 딥러닝을 배우긴 했지만 그때 그때 필요한 것들만 배우느라 기초적이거나 다른 것들을 배우지 못한 사람들에게는 아주 유용한 책인것 같아 추천합니다. 그리고 한 가지 아쉬웠던 것은 저는 자연어처리를 전공으로 했기 때문에 자연어처리와 관련된 내용보다는 이미지처리에 대한 코드들이 대부분인게 조금 아쉬웠던 것 같습니다.
긴 글 읽어주셔서 감사드리며, 잘못된 내용이나 오타, 궁금하신 사항이 있으시면 댓글 달아주시기 바랍니다.

Comments