[Deeplearning] Pytorch 를 이용한 인공 신경망
이번엔 파이토치를 이용해 기본적인 인공 신경망에 대해서 알아보도록 하겠습니다. 그와 함께 딥러닝의 여러 기초적인 개념도 한 번 살펴보도록 하겠습니다.
1. 다층 퍼셉트론
이전 포스트에서 우리는 간단하게 입력층과 출력층만 있는 단순한 회귀식에 대해서 알아보았습니다. 이를 단층 퍼셉트론(Single-layer Perceptron)이라고 합니다. 단층 퍼셉트론의 한계는 비선형적인 문제를 풀 수 없다는 것인데 대표적으로 XOR 문제가 있습니다. 1969년 Marvin Minsky 교수는 단층 퍼셉트론으로는 XOR 문제를 해결할 수 없음을 수학적으로 증명하여 AI 연구의 암흑기를 맞이했고, 많은 연구자들이 인공지능 연구를 중단하기도 했습니다. XOR 문제는 활성화 함수에 입력층과 출력층 사이에 은닉층을 추가한 다층 퍼셉트론(Multi-layer Perceptron)을 통해 해결이 가능합니다.
1.1 선형 회귀
우선 복습도 하는겸 이전 포스트에서 다루었던 선형 회귀 모델(단층 퍼셉트론)을 파이토치를 이용해 구축해보겠습니다.
x, y 데이터를 만듭니다. 이 때 각각 2차원 데이터로 표현하기 위해 unsqueeze(1)를 사용합니다.
import torch
import torch.nn as nn
from matplotlib import pyplot as plt
# 0, 1, 2, 3, 4 를 float32 텐서로 만들고 (5,) -> (5,1) 형태로 차원을 하나 늘림
# 선형회귀에서 특성행렬 X를 (N, D) 꼴로 사용하기 위해 unsqueeze(1) 사용
x = torch.FloatTensor(range(5)).unsqueeze(1)
# 타깃 y = 2*x + ε (ε ~ U[0,1)) : 실제 관계(기울기=2)에 약간의 잡음을 더해 학습 문제를 구성
y = 2*x + torch.rand(5,1)
먼저 nn.Module을 상속받는 클래스 LinearRegressor을 만듭니다.
초기 세팅에 필요한 내용을 입력하는 __init__과 super().__init__()을 적어줍니다.
선형 회귀 모델 y=wx+b를 nn.Linear(N, M, bias=True)으로 표현할 수 있습니다. N 은 입력 변수의 개수이고, M 은 출력 변수의 개수입니다. 여기서 x 의 크기가 1(N=1), y 의 크기가 1(M=1)입니다
forward 함수는 실제 입력값이 들어와 연산이 진행하는 순서와 방법을 정하는 곳입니다. 따라서 self.fc로 위에서 정의된 선형식을 사용하여 x 값을 받아 y 값을 반환하도록 합니다.
class LinearRegressor(nn.Module):
def __init__(self):
super().__init__()
# 입력 벡터의 크기가 1이고, 출력 벡터의 크기가 1인 선형 레이어 정의
self.fc = nn.Linear(1,1,bias=True)
def forward(self, x):
y = self.fc(x)
return y
클래스가 완성되었다면 model 을 선언합니다. MSE 를 손실 함수로 사용합니다. 최적화 방법에 모델 파라미터를 넣어 줄 때는 model.parameters() 라고 입력합니다.
# 모델 정의
model = LinearRegressor()
# 학습률 설정
learning_rate = 1e-3
# 손실 함수 설정
criterion = nn.MSELoss()
# 최적화 함수 설정
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
모델 학습과, 학습된 모델을 통해 예측값을 산출합니다.
# 손실 함수값을 출력하기 위해 손실값을 저장하는 리스트
loss_stack = []
for epoch in range(1001):
# 이전 step 에서 누적된 gradient 를 0으로 초기화
optimizer.zero_grad()
# 정의한 모델로 예측값과 손실값을 구한다
y_hat = model(x)
loss = criterion(y_hat, y)
# 역전파 학습 진행
loss.backward()
optimizer.step()
loss_stack.append(loss.item())
if epoch % 100 == 0:
print(f"Epoch {epoch}:{loss.item()}")
with torch.no_grad():
y_hat = model(x)
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.plot(loss_stack)
plt.title("Loss")
plt.subplot(122)
plt.plot(x, y, '.b')
plt.plot(x, y_hat, 'r-')
plt.legend(['ground truth', 'prediction'])
plt.title("Prediction")
plt.show()
1.2 집값 예측하기
선형 회귀식은 nn.Linear()가 하나 있는 모델을 의미합니다. 선형식은 모든 데이터를 직선으로 예측하기 때문에 학습이 매우 빠르다는 장점이 있습니다. 하지만 데이터 내 변수들은 일반적으로 비선형 관계를 갖기 때문에 선형 모델을 가지고 예측하는 것은 한계가 있습니다. 따라서 nn.Linear()을 줄지어 여러층으로 구성된 깊은 신경망을 만듭니다. 이를 다층 신경망(Multi-layer Perceptron)이라고 합니다. 이를 통해 대표적인 회귀 문제인 집값 예측을 합니다.
아래는 집값 예측 모델을 위한 모듈들을 import 하는 부분입니다. 우선 첫 번째 줄은 데이터프레임 형태를 다룰 수 있는 pandas 입니다. pandas 는 데이터를 데이터프레임 형태로 다룰 수 있어, 보다 안정적이고 쉽게 테이블형 데이터를 다룰 수 있습니다. 또한 다양한 통계 함수와 시각화 기능을 갖추고 있어 결과 분석에도 많이 사용되고 있습니다.
여덟 번째 줄에는 회귀 문제(Regression)의 평가를 위해 RMSE(Root Mean Squared Error)를 사용합니다. 즉, MSE(Mean Squared Error)척도를 라이브러리를 통해 불러온 후 MSE에 제곱근을 씌어 계산합니다. MSE 는 예측값과 실제값의 거리의 제곱을 이용하여 다음과 같이 정의합니다.
\[\text{MSE} \;=\; \frac{1}{n}\sum_{i=1}^{n}\bigl(y_i - \hat{y}_i\bigr)^2\]이는 미분 계산이 쉽기 때문에 머신러닝 모델을 최적화하기 위해 자주 사용되는 손실 함수입니다. 하지만 기본 단위에 제곱을 취해서 나온 척도이므로 데이터와 동일한 단위가 아닙니다. 따라서 통계적 해석을 할 때에는 단위를 맞추기 위해 MSE 에 제곱근을 씌어 RMSE 로 결과를 평가할 수 있습니다. 아래는 RMSE 수식입니다.
\[\text{RMSE} \;=\; \sqrt{ \frac{1}{n} \sum_{i=1}^{n} \bigl( y_i - \hat{y}_i \bigr)^2 }\]import pandas as pd # 데이터프레임 형태를 다룰 수 있는 라이브러리
import numpy as np
from sklearn.model_selection import train_test_split # 전체 데이터를 학습 데이터와 평가 데이터로 나눈다
import torch
from torch import nn, optim # torch 내의 세부적인 기능을 불러온다.
from torch.utils.data import DataLoader, Dataset # 데이터를 모델에 사용할 수 있도록 정리해 주는 라이브러리
import torch.nn.functional as F # torch 내의 세부적인 기능을 불러온다.
from sklearn.metrics import mean_squared_error # Regression 문제의 평가를 위해 MSE(Mean Squared Error) 를 불러온다
import matplotlib.pyplot as plt # 시각화 도구
데이터 세트 만들기
스케일링된 집값 데이터를 read_csv를 통해 불러옵니다. 이 때 index_col=[0]을 이용하여 csv 파일 첫 번째 열에 있는 데이터의 인덱스를 배제하고 데이터프레임을 만듭니다. 데이터 내의 변수의 개수가 13개이고, 인스턴스의 개수는 506개입니다.
# 주식 데이터가 있는 csv 파일을 pandas 를 이용해 읽어온다.
df = pd.read_csv("/content/drive/MyDrive/pytorch/reg.csv", index_col=[0])
데이터 프레임을 넘파이 배열로 만들기
데이터프레임 df 에서 Price 를 제외한 나머지를 변수로 사용합니다. drop 의 axis=1 은 열을 의미하여 Price 를 열 기준으로 배제하겠다는 의미입니다. 그리고 Price 를 타겟값 Y 로 사용합니다.
# 데이터를 넘파이 배열로 만들기
X = df.drop("Price", axis=1).to_numpy() # 데이터프레임에서 타겟값(Price)를 제외하고 넘파이 배열로 만들기
Y = df["Price"].to_numpy().reshape((-1,1)) # 데이터프레임 형태의 타겟값을 넘파이 배열로 만들기
전체 데이터를 50:50으로 학습 데이터와 평가 데이터로 나눕니다.
# 전체 데이터를 학습 데이터와 평가 데이터로 나눈다.
# 기준으로 잡은 논문이 전체 데이터를 50%, 50%로 나눴기 때문에 test size를 0.5로 설정한다.
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.5)
텐서 데이터 만들기
trainloader 와 testloader 를 만듭니다. 일반적으로 학습 데이터는 shuffle=True 로 주고 평가는 shuffle=False 로 설정합니다.
# 데이터를 텐서 형태로 변경 시켜주는 클래스
class TensorData(Dataset):
def __init__(self, x_data, y_data):
self.x_data = torch.FloatTensor(x_data)
self.y_data = torch.FloatTensor(y_data)
self.len = self.y_data.shape[0]
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
# 학습 데이터, 시험 데이터 배치 형태로 구축하기
trainsets = TensorData(X_train, Y_train)
trainloader = torch.utils.data.DataLoader(trainsets, batch_size=32, shuffle=True)
testsets = TensorData(X_test, Y_test)
testloader = torch.utils.data.DataLoader(testsets, batch_size=32, shuffle=False)
모델 구축하기
Regressor 는 입력층 1개, 은닉층 2개, 출력층 1개를 가진 모델입니다. 데이터 피쳐의 개수가 13이므로 입력층의 노드가 13개가 있어야 하고, 하나의 값으로 표현된 집값을 예측하는 것이므로 출력층은 1개의 노드를 가져야만 합니다. 은닉층은 사용자의 선택으로 정할 수 있는데 이 모델에서는 각 은닉층 마다 50, 30개의 노드를 갖도록 구축합니다.(기본적으로 이전 층의 출력값과 다음 층의 입력값의 크기는 같아야 합니다.)
self.fc1 = nn.Linear(13, 50, bias=True) 입력층(노드수: 13) -> 은닉층1(50)으로 가는 연산입니다.
self.fc2 = nn.Linear(50, 30, bias=True) 은닉층1(50) -> 은닉층2(30) 으로가는 연산입니다.
self.fc3 = nn.Linear(30, 1, bias=True) 은닉층2(30) -> 출력층(1)으로 가는 연산
self.dropout = nn.Dropout(0.5) 연산이 될 때마다 50%의 비율로 랜덤하게 노드를 없앱니다.(forward 함수에서 적용 위치를 정해줍니다.)
F.relu(self.fc1(x))는 선형 연산 후 ReLU 라는 활성화 함수를 적용합니다. 일반적으로 활성화 함수는 관계를 비선형으로 만들어 줄 수 있어 성능 향상에 도움이 됩니다.
self.dropout(F.relu(self.fc2(x))) 데이터가 노드가 50개인 이전 은닉층에서 30개의 은닉층으로 넘어갈 때 ReLu라는 활성화 함수를 거치고 self.dropout 을 이용해 30개 중 50%의 확률로 값을 0으로 만듭니다. dropout 은 과적합(overfitting)을 방지하기 위해 노드의 일부를 배제하고 학습하는 방식이기 때문에 사용위치는 임의로 정할 수 있지만 절대로 출력층에 사용해서는 안됩니다.
마지막으로 출력은 배치가 32개고 출력값이 하나이기 때문에 크기가 torch.Size([32, 1])인 결과를 뽑아내어 반환합니다.
class Regressor(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(13, 50, bias=True) # 입력층(13) -> 은닉층1(50)으로 가는 연산
self.fc2 = nn.Linear(50, 30, bias=True) # 은닉층1(50) -> 은닉층2(30)으로 가는 연산
self.fc3 = nn.Linear(30, 1, bias=True) # 은닉층2(30) -> 출력층(1)으로 가는 연산
self.dropout = nn.Dropout(0.5)
def forward(self, x): # 모델 연산의 순서를 정의
x = F.relu(self.fc1(x)) # Linear 계산 후 활성화 함수 ReLU를 적용한다.
x = self.dropout(F.relu(self.fc2(x))) # 은닉층2 에서 드랍아웃을 적용한다
x = F.relu(self.fc3(x)) # Linear 계산 후 활성화 함수 ReLU를 적용한다.
return x
모델 학습하기
Adam 의 최적화 방법을 정의합니다. weight_decay 는 $L_2$ 정규화에서의 penalty 값을 의미하며 값이 클수록 제약조건이 강함을 의미합니다.
model = Regressor() # 모델 정의
criterion = nn.MSELoss() # 손실 함수 정의
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-7) # 최적화 함수 정의
loss_ = [] # 손실값을 그래프로 그리기 위해 손실값을 담는 리스트
n = len(trainloader) # 배치 사이즈
for epoch in range(400):
running_loss = 0.0
for data in trainloader: # 무작위로 섞인 32개 데이터가 있는 배치가 하나씩 들어온다.
inputs, values = data
optimizer.zero_grad() # 최적화 초기화
outputs = model(inputs) # 모델에 입력값 대입 후 예측값 산출
loss = criterion(outputs, values) # 손실 함수 계산
loss.backward() # 손실 함수 기준으로 역전파 설정
optimizer.step() # 역전파를 진행하고 가중치 업데이트
running_loss += loss.item() # epoch 마다 평균 loss를 계산하기 위해 배치 loss 를 더한다.
loss_.append(running_loss/n)
손실 함수값 그리기
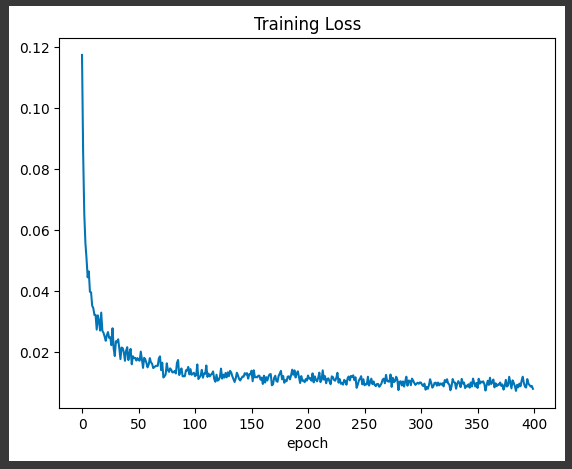
학습 데이터의 손실 함수값으로는 모델의 성능을 판단할 수 없지만, 학습이 잘 진행되었는지는 파악할 수 있습니다. 아래 그림에선 손실 함수값이 감소하는 것은 학습이 잘 진행되었다고 판단할 수 있습니다.
plt.plot(loss_)
plt.title("Training Loss")
plt.xlabel("epoch")
plt.show()
모델 평가하기
최종적인 모델 평가는 RMSE(Root Mean Square Error)를 사용합니다.
# 평가 데이터와 학습한 모델로 평가 진행
def evaluation(dataloader):
predictions = torch.tensor([], dtype=torch.float) # 예측값을 저장할 빈 텐서 정의
actual = torch.tensor([], dtype=torch.float) # 실제값을 저장하는 빈 텐서 정의
with torch.no_grad():
model.eval() # 평가를 진행할 때에는 모델이 학습하지 않도록 무조건 eval() 을 사용해야 한다.
for data in dataloader:
inputs, values = data
outputs = model(inputs)
# torch.cat 에서 0은 0번째 차원을 기준으로 누적한다는 의미이다
# 0번째 차원은 10x2, 10x2 를 누적하면 20x2로 누적됨
# 1번째 차원은 10x2, 10x2 를 누적하면 10x4로 누적됨
predictions = torch.cat((predictions, outputs), 0)
actual = torch.cat((actual, values), 0)
predictions = predictions.numpy() # 넘파이 배열로 변경
actual = actual.numpy() # 넘파이 배열로 변경
rmse = np.sqrt(mean_squared_error(predictions, actual)) # sklearn 을 이용하여 RMSE 계산
return rmse
결과를 보면 학습 결과와 테스트 결과가 차이가 큽니다. 따라서 학습 데이터에 과적합이 되어 있다고 판단할 수 있습니다. 하지만 데이터를 무작위로 나누고 모델의 초깃값도 random initial parameter 를 사용했기 때문에 학습을 할 때마다 결과가 다르게 나올 수 있습니다. 따라서 교차 검증이나 여러 번의 실험을 통해 결과의 경향성을 봐야합니다.
train_rmse = evaluation(trainloader) # 학습 데이터의 RMSE
test_rmse = evaluation(testloader) # 시험 데이터의 RMSE
print("Train RMSE:", train_rmse)
print("Test RMSE:", test_rmse)
Output:
Train RMSE: 0.07102314461238661
Test RMSE: 0.1078935584512692
2. 활성화 함수
활성화 함수는 인공 신경망에서 필수적인 요소 중 하나입니다. 따라서 활성화 함수의 종류에 따라서 성능의 변화를 줄 수 있습니다. 기본적인 활성화 함수의 역할과 종류에 대해서 알아보도록 하겠습니다.
2.1 활성화 함수가 필요한 이유
기본적으로 인공 신경망은 선형식 계산의 연속입니다.(즉, 선형 결합 형태의 함수가 합성된 형태). 이를 통해 연산을 쉽게 할 수 있으며 미분이 가능하고 미분을 쉽게 풀 수 있게 됩니다. 이 부분에서 “과연 노드 간의 관계가 항상 선형적일까?”라는 합리적인 의심을 해볼 수 있습니다. 사회, 경제, 자연 현상들을 보면 비선형적인 관계가 많다는 것을 알 수 있습니다. 따라서 비선형적인 층 사이의 관계를 표현할 수 있는 활성화 함수(Activation function)를 사용합니다. 활성화 함수 $a(x)$는 합성 함수의 일환으로 이전 노드의 값과 가중치가 계산된 값을 활성화 함수에 넣어 계산한 뒤 다음 노드로 보내게 됩니다.
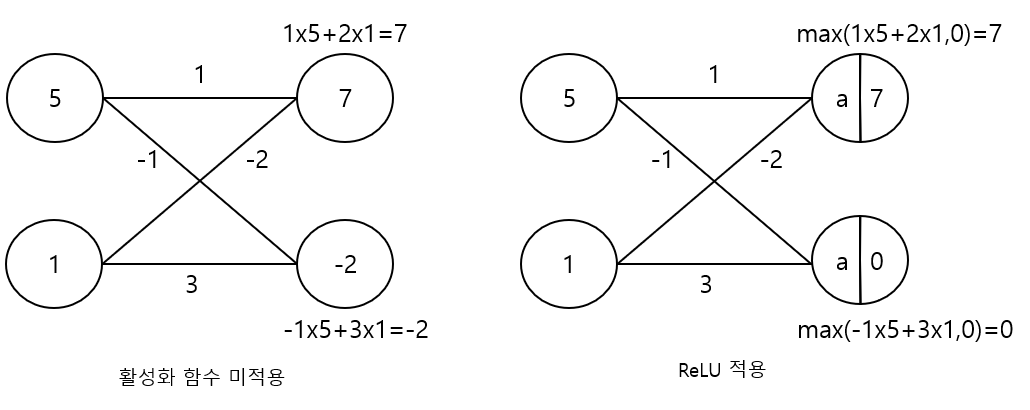
위 그림과 같이 이전 층에 있는 노드값은 가중치와 각각 곱해져 더하는 선형 결합입니다. 활성화 함수를 적용하지 않으면 계산된 값이 그대로 다음 층으로 들어갑니다. 만약 활성화 함수를 적용하다면 이전 층과 다음 층 사이에 있는 활성화 함수 $a(x)$ 를 거치게 됩니다. 만약 함수 $a(x)=max(x,0)$로 정의된 ReLU 함수를 사용했다면 음수는 모두 0으로 나오고, 양수는 계산 그대로 넘겨주게 됩니다.
2.2 선형 함수
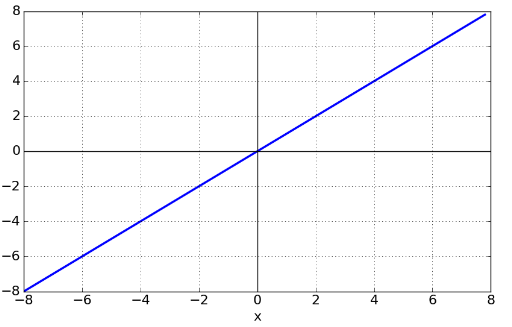
선형 함수는 $a(x)=mx+n$ 형태인 활성화 함수입니다. 만약 m=1, n=0 이면 항등 함수로써 넘어온 값을 그대로 받는다는 의미입니다. 활성화 함수의 역할은 1차적으로 비선형 관계를 만들어 주기 때문에 거의 사용하지 않습니다.
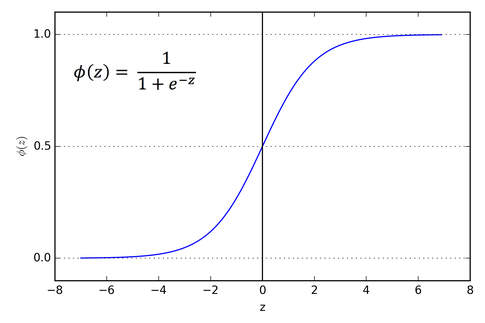
2.3 시그모이드(sigmoid) 함수 - torch.sigmoid() / nn.Sigmoid()
시그모이드 함수 $\sigma (x) = \frac{1}{1+e^{-x}}$ 는 모든 입력값에 대해 0과 1 사이로 변환하는 역할을 하며 일반적으로 $\sigma$(sigma)로 표기합니다. 또한 0.5 를 기준으로 0.5 이하면 0, 초과면 1로 변환하여 두 가지 클래스를 분류하는 이진분류(binary classification) 문제에도 활용할 수 있습니다.
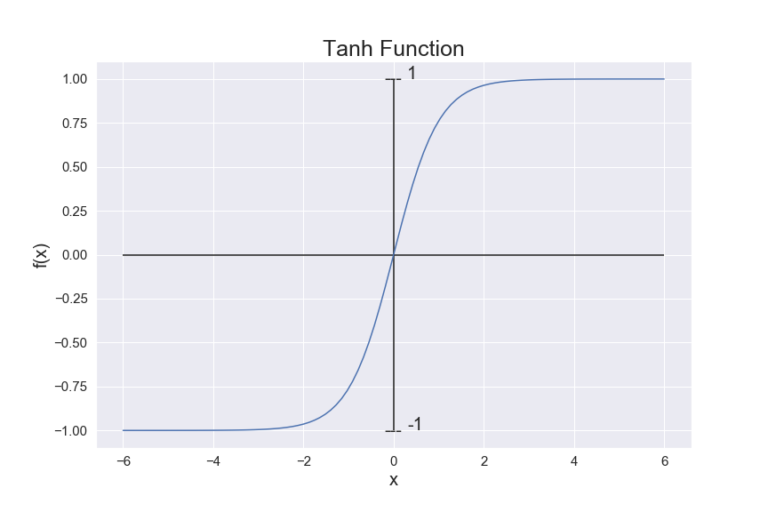
2.4 tanh 함수 - torch.tanh() / nn.Tanh()
시그모이드 함수와 형태는 유사하지만 -1과 1 사이의 값을 취할 수 있어 0과 음수값을 가질 수 있습니다. 또한 0 부근에서 시그모이드 보다 더 가파른 기울기를 갖는다는 것이 차이점입니다.
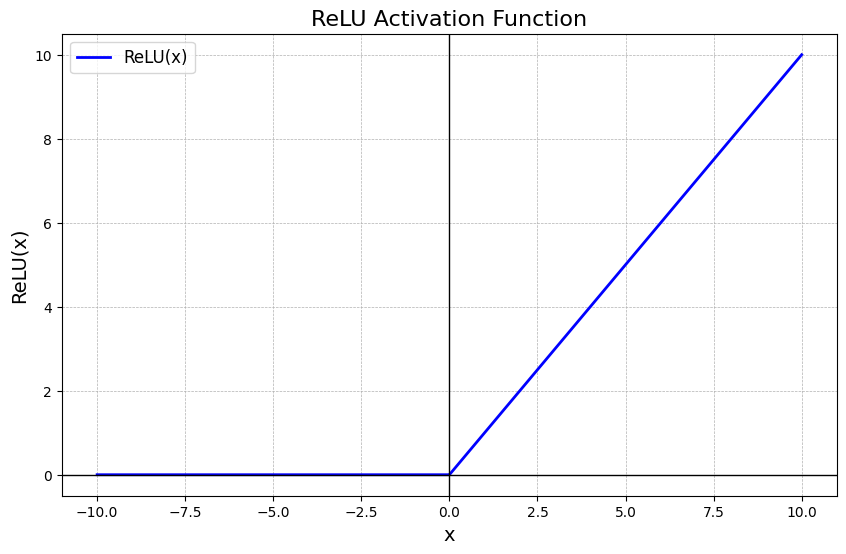
2.5 ReLU 함수 - torch.nn.functional.relu() / nn.ReLU()
두개의 직선을 이어 만든 것으로 비선형 함수지만 선형과 매우 유사한 성질을 가지고 있습니다. 따라서 계산이 쉽고 미분도 쉽게 풀 수 있습니다. 또한 가장 중요한 점은 모델 최적화에 유용한 선형적 성질들을 보존하고 있어서 최적화를 쉽게 할 수 있게 합니다. 따라서 가장 널리 사용되며 성능이 매우 좋은 것으로 알려져 있습니다.
2.6 softmax 함수 - torch.nn.functional.softmax() / nn.Softmax()
벡터 $\mathbb{x} = (x_1, x_2, \cdots, x_n)$에 대하여 모든 성분이 항상 양수이며, 그 합이 1이 되도록 변환합니다. 따라서 음수값이 오더라도 항상 양수가 나오도록 지수 함수를 이용한 함수입니다. 베겉 형태로 예측값이 나오는 다중 분류문제에서 자주 사용됩니다.
\[\sigma(\mathbb{x}) = \frac{e^{\mathbb{x}}}{\sum_{j=1}^{n} e^{x_j}}\]2.7 기타 활성화 함수
파이토치에서는 nn.ELU(), nn.LeakyReLU(), nn.LogSigmoid(), nn.SELU() 와 같은 매우 다양한 함수를 제공하고 있으며, 필요에 따라 직접 활성화 함수를 만들기도 합니다.
3. 손실 함수
손실 함수는 최적화를 하는데 목적 함수가 되기 때문에 문제에 맞는 손실 함수를 사용해야만 합니다. 또한 필요에 따라 손실 함수를 2개 이상 운용하는 모델도 있으며 가중치를 주어 특정 조건에 대해서 손실 함수값을 조정하는 방법도 있습니다. 그러면 가장 자주 사용되는 손실 함수에 대해서 알아보도록 하겠습니다.
3.1 MAE(Mean Absolute Error) - torch.nn.L1Loss
절대값 오차의 평균으로 유사도, 거리 측정, 회귀 문제 등에 많이 사용되는 손실 함수입니다. 특히 이상치가 많은 데이터, 비용 함수가 선형 페널티여야 할 때 사용하는 손실 함수 입니다.
\[\mathrm{MAE}=\frac{1}{n}\sum_{i=1}^{n}\lvert y_i-\hat{y}_i\rvert\]3.2 MSE(Mean Squared Error) - torch.nn.MSELoss
MAE 와 함께 유사도, 거리 측정, 회귀 문제 등에 많이 사용되는 손실 함수입니다. MAE 와의 차이는 MSE 는 큰 오차에 강한 벌점이 필요하거나, 미분 가능하고 매끄러운 손실이 학습에 유리할 때 주로 사용합니다.
\[\text{MSE} \;=\; \frac{1}{n}\sum_{i=1}^{n}\bigl(y_i - \hat{y}_i\bigr)^2\]3.3 Cross Entroypy Loss
주로 다중 분류 문제에서 사용되며, 분류에서 모델이 정답 클래스에 높게, 오답에는 낮게 확률을 주도록 학습시키는 손실 함수 입니다. 유의할 점은 파이토치에서는 예측값은 벡터 형태, 타깃값은 라벨 형태로 세팅해야 에러가 나지 않습니다.
\[CE = -\frac{1}{n}\sum_{i=1}^{n} y_i \log \frac{e^{\hat y_i}}{\sum_{j=1}^{n} e^{\hat y_j}}\]4. 최적화 기법
인공 신경망은 예측한 값과 타깃값을 정량적으로 비교할 수 있는 손실 함수를 통해 모델을 평가할 수 있습니다. 따라서 일반적으로 손실 함수값이 작다는 의미는 예측값과 타깃값의 차이가 작다라는 의미이므로 손실 함수값이 작게 나오게 하는 모델의 변수를 구하는 것이 최적화의 목적입니다. 그림과 같이 손실 함수가 그려져 있고 현재 모델의 변수가 $w_o$ 라고 한다면 손실 함수값이 가장 작게 나오게 하는 변수 $w^*$ 를 찾는게 목적이 되는 것입니다. 직관적으로 경사가 떨어지는 방향으로 간다면 우리가 원하는 이상적인 값을 얻을 수 있습니다. 이를 경사하강법(Gradient Descent)이라고 합니다.
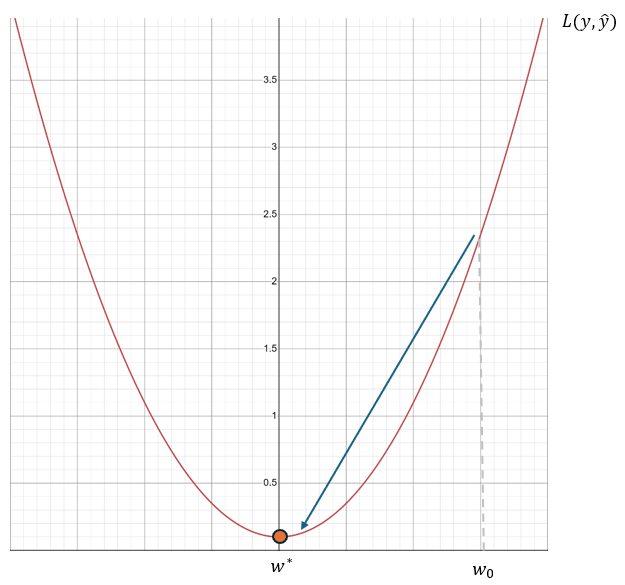
경사를 의미하는 미분을 이용해 $w$ 를 업데이트 하는데, 이 때 하강에 대한 보폭을 정해주는 값이 학습률(Learning rate 또는 Step size)입니다.
\[w \leftarrow w - \mu\frac{\partial L}{\partial w}\]최적화 문제는 깊게 들어가면 복잡한 수식과 증명들을 볼 수 있습니다. 다행히 파이토치는 계산을 자동으로 해주는 다양한 최적화 기법들을 제공하기 때문에 최적화 기법에 대한 하이퍼파라미터(Hyper-Parameter)만 신경써주면 됩니다. 하이퍼 파라미터란 제안된 방법론을 사용하기 위해 미리 선택하여 사용되는 변수를 의미하며, 예를 들면 학습률이 있습니다.
4.1 확률적 경사하강법(SGD) - torch.optim.SGD
경사하강법의 특징은 모든 변수의 미분을 계산해 한 번에 갱신한다는 것입니다. 따라서 노드 수와 가중치 수 그리고 데이터가 많을 경우에는 연산량이 많아 모델의 학습 속도가 느려지며, 계산에 필요한 메모리가 부족한 경우가 발생할 수 있습니다. 이를 해결하기 위해 데이터를 나눠서 학습하는 방법이 널리 쓰입니다. 만약 n 개의 데이터가 있다면 임의로 k 개의 데이터 묶음을 만들어 학습을 진행합니다. 이 때 나눠진 데이터 세트를 미니 배치라고 하며, 미니 배치를 이용해 경사하강법을 진행하는 것을 확률적 경사하강법(Stochastic Gradient Descent)이라고 합니다. 따라서 일반 경사하강법과 SGD 의 차이는 데이터 전체를 한 번에 사용하는지 나눠서 사용하는지의 차이일 뿐, 계산 과정의 차이는 없습니다. 또한 “확률적”이라고 하는 이유는 미니 배치를 나눌 때 데이터를 무작위로 섞어서 나누기 때문입니다.
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
4.2 다양한 최적화 기법
경사하강법과 SGD 의 단점은 학습률이 고정되어 있다는 것입니다. 따라서 변수의 위치에 상관없이 이동 비율이 항상 같기 때문에 계산이 비효율적일 수 있습니다. 따라서 더 효율적인 최적화를 위해 여러가지 방법들이 고안되었습니다. 그 중 기본적으로 많이 사용되는 방법은 모멘텀 + 스케쥴링이나 Adam 입니다.
4.3 스케쥴링
가변 학습률을 사용하지 않는 방법에 대해서는 학습률이 변하지 않습니다. 따라서 별도로 학습률이 어떻게 바뀌는지 규칙을 정해주는 것을 스케쥴링이라고 합니다. 예를 들어 학습 반복 30번마다 학습률을 0.1배씩 줄여주고 싶다면 optim.lr_scheduler.StepLR을 optimizer 아래 선언할 수 있습니다. 그리고 for 문 안에 shceduler.step()만 추가하면 자동으로 학습률을 변경해 줍니다.
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
for epoch in range(400):
running_loss = 0.0
for data in trainloader:
inputs, values = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, values)
loss.backward()
optimizer.step()
scheduler.step()
파이토치는 MultiplicativeLR, LambdaLR, StepLR, MultiStepLR, ExponentialLR, CosineAnnealingLR 등 다양한 스케줄링을 제공합니다.
4.4 MADGRAD
MADGRAD 는 모멘텀과 가변식 방법을 병행하는 최신 최적화 방법으로 SGD 와 Adam 을 능가하는 것으로 페이스북 연구팀이 발표한 바 있습니다.
5. 교차검증
기본적인 모델의 학습과 평가 과정은 학습 데이터로 학습하고 평가 데이터로 성능을 확인합니다. 이 때 평가 데이터에서 가장 성능이 잘 나오는 모델을 고르게 됩니다. 학습 시 평가 데이터를 사용하지 않기 때문에 평가 방법에 문제가 되지 않는다고 생각할 수 있지만, 평가 데이터를 기준으로 모델을 튜닝한다면 모델이 평가 데이터에 과적합이 될 수 도 있습니다. 물론 빠르게 작업할 수 있으며, 어느 정도 성능은 충분히 가늠할 수 있기 때문에 많이 사용됩니다. 하지만 앞에서 언급한 단점을 보완하기 위해 검증 데이터를 사용합니다. 전체 데이터를 학습, 검증, 평가 데이터로 나누어 학습 데이터로 모델을 학습하고 검증 데이터로 모델을 평가하고 튜닝한 다음 평가 데이터로 최종 평가를 합니다. 데이터를 나누는 방법은 매우 다양합니다. 그 중 k겹 교차 검증(k-Fold Cross-validation)은 학습 데이터 전체를 사용하면서 검증할 수 있는 방법으로 머신러닝 분야에서 매우 널리 쓰이는 검증 방법입니다. 학습 데이터를 k 개로 나누어 1개는 검증 데이터로 사용하고 나머지 k-1 개는 학습 데이터로 사용합니다. 따라서 k 번의 검증 과정이 필요하기 때문에 느린 것이 단점입니다. 그럼 이전에 진행했던 MLP 모델을 이용해 교차 검증을 진행해 보도록 하겠습니다.
5.1 교차 검증을 통한 집값 예측 모델 평가
모듈 임포트 하기
from skealrn.model_selection import KFold 는 학습 데이터 세트를 k개의 부분 데이터 세트(폴드)로 나눈 후 k-1 개의 폴드는 학습 데이터로 사용하고, 나머지 1개는 검증 데이터로 사용할 수 있도록 전체 학습 데이터 세트에서 인덱스를 나눠주는 역할을 합니다.
import pandas as pd # 데이터프레임 형태를 다룰 수 있는 라이브러리
import numpy as np
from sklearn.model_selection import train_test_split # 전체 데이터를 학습 데이터와 평가 데이터로 나눈다.
# ANN
import torch
from torch import nn, optim # torch 내의 세부적인 기능을 불러온다. (신경망 기술, 손실함수, 최적화 방법 등)
from torch.utils.data import DataLoader, Dataset # 데이터를 모델에 사용할 수 있도록 정리해 주는 라이브러리
import torch.nn.functional as F # torch 내의 세부적인 기능을 불러온다. (신경망 기술 등)
# Cross Validation
from sklearn.model_selection import KFold
# Loss
from sklearn.metrics import mean_squared_error # Regression 문제의 평가를 위해 MSE(Mean Squared Error)를 불러온다.
# Plot
import matplotlib.pyplot as plt # 시각화 도구
데이터 프레임을 넘파이 배열로 만들기
이전에 사용했던 스케일링된 집값 데이터를 read_csv 를 통해 불러옵니다. 이 때 index_col=[0]을 이용하여 csv 파일의 첫 번째 열에 있는 데이터의 인덱스를 배제하고 데이터프레임을 만듭니다. 데이터프레임 df 에서 Price 를 제외한 나머지를 변수로 사용합니다. drop 의 axis=1 은 열을 의미하여 Price 를 열 기준으로 배제하겠다는 의미입니다. Price 를 타겟값 Y 로 사용합니다.
df = pd.read_csv("/content/drive/MyDrive/pytorch/reg.csv", index_col=[0])
X = df.drop("Price", axis=1).to_numpy()
Y = df["Price"].to_numpy().reshape((-1,1))
텐서 데이터 만들기
trainset 은 교차 검증을 위해 나누기 대문에 미리 DataLoader 를 정의하지 않습니다.
# 텐서 데이터로 변환하는 클래스
class TensorData(Dataset):
def __init__(self, x_data, y_data):
self.x_data = torch.FloatTensor(x_data)
self.y_data = torch.FloatTensor(y_data)
self.len = self.y_data.shape[0]
def __getitem__(self, index):
return self.x_data[index], self.y_data[index]
def __len__(self):
return self.len
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.7)
trainset = TensorData(X_train, Y_train)
testset = TensorData(X_test, Y_test)
testloader = DataLoader(testset, batch_size=32, shuffle=False)
모델 구축
class Regressor(nn.Module):
def __init__(self):
super().__init__() # 모델 연산 정의
self.fc1 = nn.Linear(13, 50, bias=True) # 입력층(13) -> 은닉층1(50)으로 가는 연산
self.fc2 = nn.Linear(50, 30, bias=True) # 은닉층1(50) -> 은닉층2(30)으로 가는 연산
self.fc3 = nn.Linear(30, 1, bias=True) # 은닉층2(30) -> 출력층(1)으로 가는 연산
def forward(self, x):
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
return x
손실 함수와 교차 검증 정의
학습 데이터를 3개의 폴드로 나누어 3겹 교차 검증을 진행합니다.
kfold = KFold(n_splits=3, shuffle=True)
criterion = nn.MSELoss()
평가 함수 정의
def evaluation(dataloader):
predictions = torch.tensor([], dtype=torch.float) # 예측값을 저장하는 텐서
actual = torch.tensor([], dtype=torch.float) # 실제값을 저장하는 텐서
with torch.no_grad():
model.eval() # 평가를 할 때에는 .eval() 반드시 사용해야 한다.
for data in dataloader:
inputs, values = data
outputs = model(inputs)
predictions = torch.cat((predictions, outputs), 0) # cat을 통해 예측값을 누적
actual = torch.cat((actual, values), 0) # cat을 통해 실제값을 누적
predictions = predictions.numpy() # 넘파이 배열로 변경
actual = actual.numpy() # 넘파이 배열로 변경
rmse = np.sqrt(mean_squared_error(predictions, actual)) # sklearn을 이용하여 RMSE 계산
model.train()
return rmse
# 평가 시 .eval()을 사용해야 하는 이유
# 이번 예시에서는 상관없으나 평가 시에는 정규화 기술을 배제하여 온전한 모델로 평가를 해야한다. 따라서 .eval()을 사용한다.
# 즉, 드랍아웃이나 배치 정규화 등과 같이 학습 시에만 사용하는 기술들이 적용 된 모델은 평가 시에는 비활성화 해야하며 학습 시 .train()을 사용한다.
교차 검증을 이용한 학습 및 평가
validation_loss = [] 검증 점수를 산출하기 위해 폴드 별 로스 저장 리스트를 만듭니다.
Kfold.split(trainset) 을 이용하여 나눠진 학습 데이터의 인덱스를 불러옵니다.
TensorData 로 정의된 데이터의 일부를 불러와 배치 데이터 형태로 활용할 수 있도록 DataLoader 와 SubsetSampler 를 함께 사용합니다.
validation_loss = []
for fold, (train_idx, val_idx) in enumerate(kfold.split(trainset)):
train_subsampler = torch.utils.data.SubsetRandomSampler(train_idx) # index 생성
val_subsampler = torch.utils.data.SubsetRandomSampler(val_idx) # index 생성
# sampler를 이용한 DataLoader 정의
trainloader = torch.utils.data.DataLoader(trainset, batch_size=32, sampler=train_subsampler)
valloader = torch.utils.data.DataLoader(trainset, batch_size=32, sampler=val_subsampler)
# 모델
model = Regressor()
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-7)
for epoch in range(400): # 400번 학습을 진행한다.
for data in trainloader: # 무작위로 섞인 32개 데이터가 있는 배치가 하나 씩 들어온다.
inputs, values = data # data에는 X, Y가 들어있다.
optimizer.zero_grad() # 최적화 초기화
outputs = model(inputs) # 모델에 입력값 대입 후 예측값 산출
loss = criterion(outputs, values) # 손실 함수 계산
loss.backward() # 손실 함수 기준으로 역전파 설정
optimizer.step() # 역전파를 진행하고 가중치 업데이트
train_rmse = evaluation(trainloader) # 학습 데이터의 RMSE
val_rmse = evaluation(valloader)
print("k-fold", fold," Train Loss: %.4f, Validation Loss: %.4f" %(train_rmse, val_rmse))
validation_loss.append(val_rmse)
validation_loss = np.array(validation_loss)
mean = np.mean(validation_loss)
std = np.std(validation_loss)
print("Validation Score: %.4f, ± %.4f" %(mean, std))
Output:
k-fold 0 Train Loss: 0.0899, Validation Loss: 0.1220
k-fold 1 Train Loss: 0.1014, Validation Loss: 0.0994
k-fold 2 Train Loss: 0.1031, Validation Loss: 0.1008
검증 점수 산출
validation_loss = np.array(validation_loss)
mean = np.mean(validation_loss)
std = np.std(validation_loss)
print("Validation Score: %.4f ± %.4f" %(mean, std))
Output: Validation Score: 0.1074 ± 0.0103
모델 평가
trainloader = torch.utils.data.DataLoader(trainset, batch_size=32, shuffle=True)
train_rmse = evaluation(trainloader)
test_rmse = evaluation(testloader)
print("Train RMSE: %.4f" %train_rmse)
print("Test RMSE: %.4f" %test_rmse)
Output:
Train RMSE: 0.1024
Test RMSE: 0.1345
6. 모델 구조 및 가중치 확인
모델 튜닝에 필요한 모델 구조 및 가중치를 확인하는 방법에 대해서 알아봅니다.
6.1 모델 구조
torchsummary 는 구조와 모델 변수를 간략히 알려주는 라이브러리입니다. pip install torchsummary을 통해 별도의 설치가 필요합니다.
import torch
from torch import nn
import torch.nn.functional as F
from torchsummary import summary
모델을 보면 변수가 있는 곳은 nn.Linear 가 있는 부분입니다. 입력층에서 첫 번째 은닉층으로 넘어가는 부분의 가중치는 13x50=650 개, 편향이 50개 이므로 총 700개의 변수가 존재합니다. 첫 번째 은닉층에서 두 번째 은닉층 사이에는 가중치가 50x30=1500개, 편향이 30개이므로 변수가 총 1530개이고 마지막 출력층으로 가는 길목에는 가중치 30개, 편향 1개를 포함해 총 31개가 존재합니다.
class Regressor(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(13, 50) # 입력층(13) -> 은닉층(50)
self.fc2 = nn.Linear(50, 30) # 은닉층(50) -> 은닉층(50)
self.fc3 = nn.Linear(30, 1) # 은닉층(30) -> 출력층(1)
self.dropout = nn.Dropout(0.5)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.dropout(F.relu(self .fc2(x)))
x = F.relu(self.fc3(x))
return x
모델을 출력하면 __init__ 부분에서 정의된 구조를 확인할 수 있습니다.
model = Regressor()
print(model)
Output:
Regressor(
(fc1): Linear(in_features=13, out_features=50, bias=True)
(fc2): Linear(in_features=50, out_features=30, bias=True)
(fc3): Linear(in_features=30, out_features=1, bias=True)
(dropout): Dropout(p=0.5, inplace=False)
)
6.2 모델 변수
model.parameters() 를 통해 정의된 순서대로 변수를 얻을 수 있습니다.
for parameter in model.parameters():
print(parameter.size())
Output:
torch.Size([50, 13])
torch.Size([50])
torch.Size([30, 50])
torch.Size([30])
torch.Size([1, 30])
torch.Size([1])
변수명을 알고 있다면 직접 접근하여 변수를 불러올 수 있습니다. 예를 들어 model 에 fc1 의 가중치를 불러 오고 있다면 model.fc1.weight 이라고 작성하고, 편향은 model.fc1.bias 라고 작성합니다.
print(model.fc1.weight.size(), model.fc1.bias.size())
Outupt: torch.Size([50, 13]) torch.Size([50])
변수명을 모를 경우에는 model.named_parameters()을 통해 변수명과 변수를 동시에 불러올 수 있습니다.
for name, param in model.named_parameters():
print(name, param.size())
Output:
fc1.weight torch.Size([50, 13])
fc1.bias torch.Size([50])
fc2.weight torch.Size([30, 50])
fc2.bias torch.Size([30])
fc3.weight torch.Size([1, 30])
fc3.bias torch.Size([1])
torchsummary에서 제공하는 summary 에 model 을 넣고 임의의 입력 데이터 사이즈를 넣으면 층마다 출력값의 크기와 변수에 대한 정보를 테이블로 만들어줍니다.
summary(model, (10, 13))
Output:
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Linear-1 [-1, 10, 50] 700
Linear-2 [-1, 10, 30] 1,530
Dropout-3 [-1, 10, 30] 0
Linear-4 [-1, 10, 1] 31
================================================================
Total params: 2,261
Trainable params: 2,261
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 0.01
Estimated Total Size (MB): 0.02
----------------------------------------------------------------
마치며
파이토치를 이용한 인공 신경망인 MLP 에 대해서 알아보고, 학습과 평가 시에 사용하는 기초적인 여러 개념들과 기법들에 대해서 알아보았습니다. 추후에 여러가지 경사하강법들과 손실 함수에 대해서 더 알아보고자 합니다. 긴 글 읽어주셔서 감사드리며, 잘못된 내용이나 오타 혹은 궁금하신 사항이 있으시면 댓글 달아주시기 바랍니다.

Comments