[Deeplearning] 파이토치를 이용한 비지도 학습 알아보기

이번엔 파이토치를 이용해 비지도 학습에 대해서 알아보도록 하겠습니다. 우리가 실제 데이터를 이용하여 모델을 구축하고 데이터를 분석한다고 가정할 때 가장 어려운 부분은 데이터 수집 및 가공입니다. 학습용으로 다루는 데이터들은 일반적으로 양도 충분하고 정답도 있어 지도 학습을 진행할 수 있습니다. 하지만 정답이 없는 경우에는 지도 학습을 위해 데이터 전체에 정답을 달아줘야 합니다. 이 때 데이터가 많다면 시간과 비용이 많이 들고 상황에 따라서는 정답을 어떻게 줘야 할지 애매한 경우가 있습니다. 또한 실수로 정답을 잘못 매기는 경우도 생길 수 있습니다. 비지도 학습은 정답 없이 데이터의 특성을 파악하는 학습 방법입니다. 즉, 모델에게 정답을 알려주지 않기 때문에 라벨링이 없는 데이터를 사용할 수 있다는 장점이 있습니다. 하지만 정답을 모르기 때문에 상대적으로 지도 학습보다는 성능이 낮을 수 있습니다. 대표적인 비지도 학습의 종류로는 입력 데이터로부터 특성을 뽑아 유사 성질들을 군집화 하는 클러스터링(Clustering)과 새로운 데이터를 생성해 내는 오토인코더(Autoencoder)와 생성적 적대 신경망(GAN)이 있습니다.

1. K-평균 알고리즘

클러스터링은 입력 데이터로부터 특성을 뽑아 유사 성질들을 군집화하는 비지도 학습이며 종류가 매우 다양합니다. 정답이 없어 클러스터링 종류에 따라 군집을 다르게 할 수 있기 때문에 종류 선택과 각 알고리즘의 하이퍼 파라미터 값을 잘 따져 봐야 합니다. K-평균(K-means) 알고리즘은 각 클러스터의 평균을 기준으로 점들을 배치시키는 알고리즘입니다. 이 때, 특정 거리 함수를 통해 각 중심(Centroid)과 입력값의 거리를 측정하고 그 중 가장 가까운 그룹으로 할당을 합니다. 예를 들어 그룹이 3개라면 각 그룹의 중심이 3개가 있고 어떤 한 점과 중심과의 거리를 계산합니다. 이 때 첫 번째 중심과의 거리가 가장 가까웠다면 이 점은 첫 번째 그룹으로 귀속됩니다. 모든 점이 할당되면 각 그룹의 평균을 구해 중심을 업데이트하고 위 과정을 반복하여 클러스터링을 시행합니다.

1.1 데이터 만들기

sklearn.datasets 에는 다양한 데이터를 제공합니다. 이번 K-means 예제에서는 make_circles 를 이용합니다. 총 500개의 점을 생성합니다.

import torch
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles

# sklearn.datasets 에서 [500, 2] 데이터를 가져옴
x, y = make_circles(n_samples=500, noise=0.1)
plt.figure(figsize=(9,6))
plt.scatter(x[:,0], x[:,1], c=y)
plt.show()

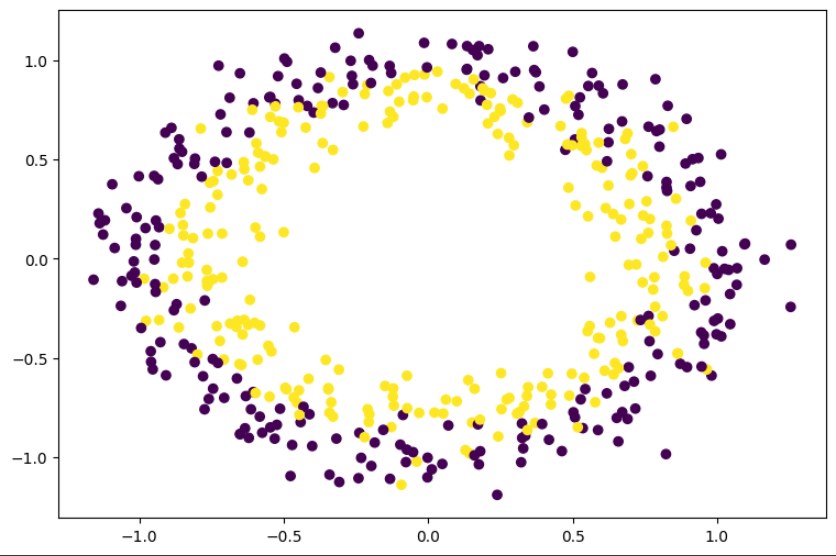
1.2 텐서 데이터 변환하기

x = torch.FloatTensor(x)

1.3 K-평균 알고리즘

거리 함수를 정의합니다. 여기서는 L2 거리 함수로 두 점(중심과 각 점)들의 거리를 측정합니다. 각 점과 중심과의 거리를 계산하여 가장 거리가 가까운 점의 인덱스를 반환합니다.

# 입력 x 와 중심점들과의 거리를 구하고, 그 중 가장 가까운 중심점의 index 를 return
def l2distance(x, centroids):
    return torch.argmin(torch.sum((x-centroids)**2, dim=1), dim=0)

K-평균 알고리즘에서는 클러스터의 수를 정해줘야만 합니다. 따라서 군집의 수를 알 수 없을 때 적절한 숫자를 찾아야 합니다. 여기서는 기본값을 num_clusters=2 로 했고, max_iteration 은 중심이 업데이트 횟수를 의미하며, 기본값을 5로 설정했습니다.

centroids = torch.rand(num_clusters, x.size(1)).to(device) 초기 중심을 랜덤으로 할당합니다. 하나의 벡터 크기는 입력값의 피쳐 개수 x.size(1)와 같아야 합니다.

h = x[m].expand(num_clusters, -1) 은 입력값 하나를 각 중심까지의 거리를 구해야 하므로 중심점의 개수 만큼 확장하기 위해 expand 를 이용해 입력값을 중심점의 개수 즉 클러스터 개수 만큼 복사하여 확장합니다.

모든 입력값과 모든 중심과의 거리를 계산하여 가장 가까운 그룹으로 할당합니다. 만약 클러스터의 개수가 2개라면 어떤 입력값과 2개의 중심점과 비교한 후 첫 번째 중심점과 가깝다면 첫 번째 그룹으로 할당합니다.

지정한 max_iteration 만큼 업데이트를 진행하며, 할당된 그룹에 있는 점들의 평균값으로 각 중심점을 업데이트 합니다.

def kmeans(x, num_clusters=2, max_iteration=5):
    """
    Args 
        x : 입력
        num_clusters : 클러스터 개수
        max_iteration : 최대 반복 횟수
    """
    device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
    x = x.to(device)

    # 클러스터 개수 만큼 랜덤 값을 가지는 중심점을 만듦 (num_clusters, 2)
    centroids = torch.rand(num_clusters, x.size(1)).to(device)
    for update in range(max_iteration):

        # 중심점에 따라 그룹을 나누기 위한 리스트
        y_assign = []
        for m in range(x.size(0)):
            h = x[m].expand(num_clusters, -1)
            assign = l2distance(h, centroids)
            y_assign.append(assign.item())

        y_assign = np.array(y_assign)
        if update != max_iteration-1:
        for i in range(num_clusters):
            idx = np.where(y_assign==i)[0]

            # 중심점으로 모인 입력값의 평균값으로 중심점을 업데이트
            centroids[i] = torch.mean(x[idx], dim=0)
    

    return y_assign, centroids

1.4 알고리즘 실행 및 그래프 그리기

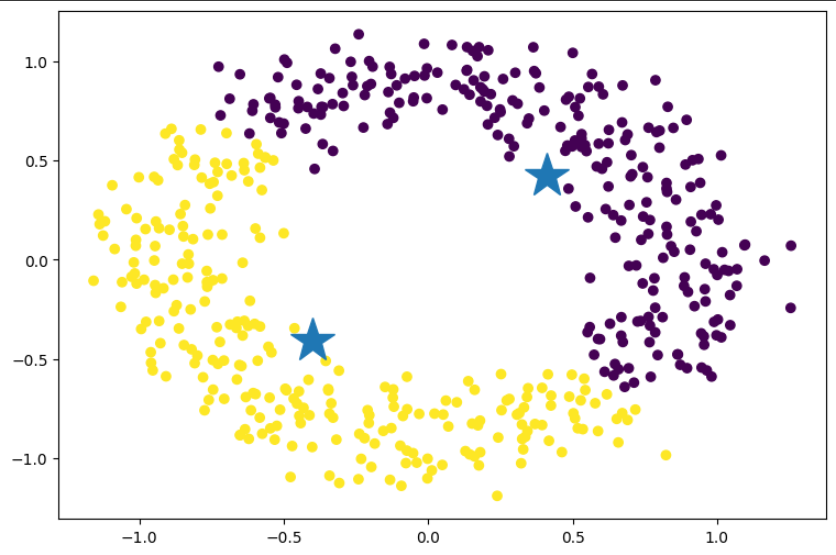
K-평균 알고리즘은 sklearn 에서 제공하는 from sklearn.cluster import KMeans 가 많이 사용됩니다. 하지만 파이토치를 통해 코드를 작성한다면 추후에 GPU 연산도 할 수 있으며 requires_grad 를 사용하여 다른 모델과 조합할 경우 역전파도 이용할 수 있습니다. 아래 이미지에서 별로 찍힌 것이 군집된 점들의 중심점입니다.

y_pred, centroids = kmeans(x,2)
plt.figure(figsize=(9,6))
plt.scatter(x[:,0], x[:,1], c=y_pred)
plt.plot(centroids[:,0].cpu(), centroids[:,1].cpu(), '*', markersize=30)
plt.show()

2. 오토인코더

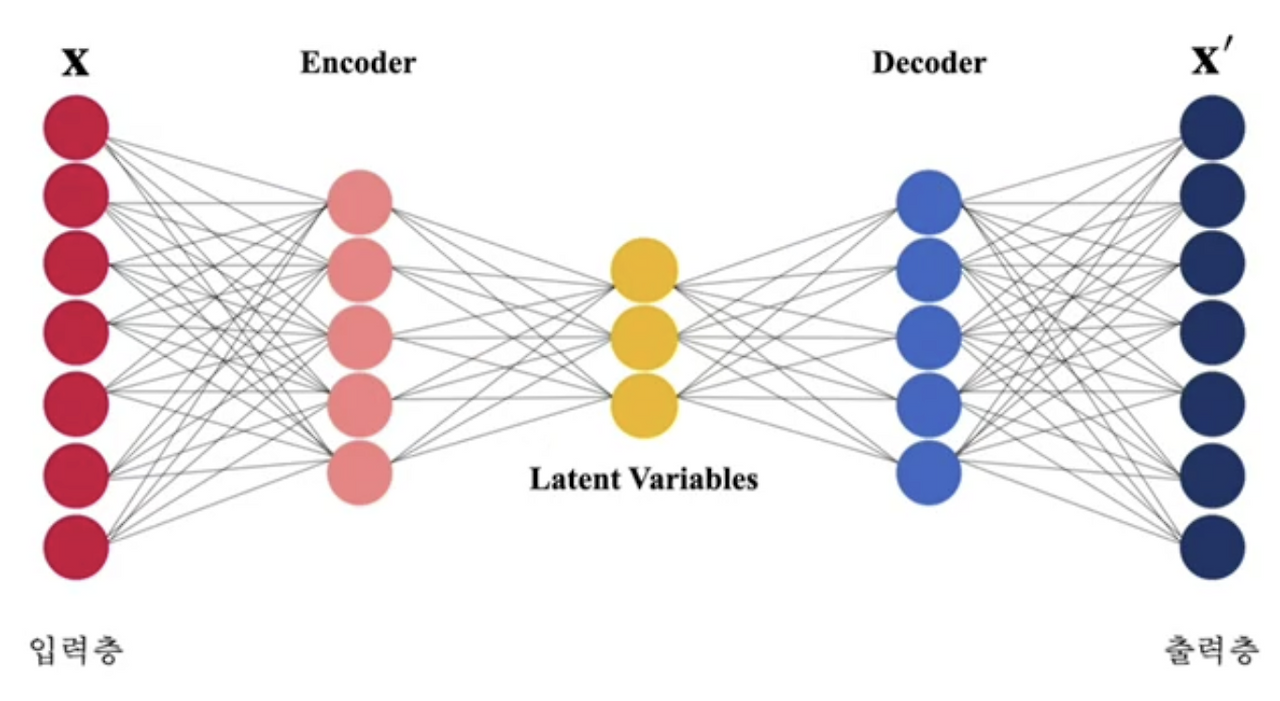
오토인코더는 정답 없이 모델을 학습시키는 비지도 학습 모델입니다. 일반적으로 대칭형 구조를 지니고 있으며, 입력 데이터를 압축하는 인코더(Encoder) 부분과 압축을 푸는 디코더(Decoder) 부분으로 구성되어 있습니다. 따라서 인코더를 통해 차원 축소가 된 잠재 변수(Latent variable)를 가지고 별도로 계산을 할 수도 있고 디코더를 통해 입력값과 유사한 값을 생성할 수도 있습니다. 기본적으로 입력값 x 와 출력값 $\acute{x}$ 를 이용하여 MSE 를 정의하고 이를 기준으로 학습을 진행합니다.

2.1 스택 오토인코더

라이브러리 불러오기

import torch
import torchvision
from torchvision import transforms
import torch.nn.functional as F
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

GPU 연산 정의 및 MNIST 데이터 불러오기

torchvision.datasets.MNIST를 이용해 데이터를 불러오고 transforms 를 이용하여 텐서 데이터로 변환합니다.

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
dataset = torchvision.datasets.MNIST(root="./data/", download=True, train=True, transform=transforms.ToTensor())
trainloader = torch.utils.data.DataLoader(dataset, batch_size=50, shuffle=True)

모델 구축하기

기본 오토인코더 모델은 층을 여러개 쌓았다고 해서 스택 오토인코더(Stacked Autoencoder)라고도 불립니다.

인코더와 디코더를 각각 nn.Sequential 로 묶어 보기 좋게 합니다.

MNIST 이미지의 크기는 1x28x28 입니다. 따라서 nn.Linear 에 넣어주기 위해 사진을 일렬로 편 후 인코더 부분에 크기가 784(28x28)인 벡터 하나가 들어오게 됩니다.

인코더에서는 층을 자유롭게 쌓아 노드를 10개까지 줄입니다. 즉, 잠재 변수의 크기가 10으로 정의됩니다.

디코더에서는 크기가 줄어든 잠재 변수 벡터를 다시 크기를 늘려줍니다.

마지막은 같은 크기의 이미지가 나와야 하므로 28*28로 입력합니다.

MNIST 이미지의 픽셀값은 0이상 1이하입니다. 따라서 nn.Sigmoid() 를 이용해 범위를 정해서 수렴을 빨리 하게 할 수 있습니다.

forward 함수에서는 encoder 와 decoder 를 차례대로 연산할 수 있도록 코드를 작성합니다.

class Autoencoder(nn.Module):
    def __init__(self):
        super(Autoencoder, self).__init__()

        # 1. 인코더
        # 28x28 벡터를 일렬 벡터로 바꾼 입력(784)를 받아 10으로 압축시킴
        self.encoder = nn.Sequential(
                    nn.Linear(784, 128),
                    nn.ReLU(),
                    nn.Linear(128, 32),
                    nn.ReLU(),
                    nn.Linear(32, 10),
                    nn.ReLU())
        # 2. 디코더
        # 인코더의 출력값을 이용해 다시 입력 이미지와 같은 크기의 784크기를 가지는 출력벡터를 생성
        self.decoder = nn.Sequential(
                    nn.Linear(10, 32),
                    nn.ReLU(),
                    nn.Linear(32, 128),
                    nn.ReLU(),
                    nn.Linear(128, 28*28),
                    nn.Sigmoid())

    def forward(self, x):
        encoded = self.encoder(x)
        decoded = self.decoder(encoded)
        return decoded

모델, 손실 함수, 최적화 기법 정의하기

우리의 목적은 입력 이미지와 유사한 출력 이미지를 얻는 것입니다. 따라서 입력 이미지와 출력 이미지의 L2 거리를 계산하는 MSE 손실 함수를 사용하고, 최적화 방법은 Adam 을 사용합니다.

model = Autoencoder().to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-4)

학습하기

현재 오토인코더의 층은 합성곱 층이 아니고 일렬 노드로 구성된 nn.Linear 입니다. 따라서 이미지를 일렬로 펴서 넣어주기 위해 outputs = model(inputs.view(-1, 28*28)) 에서 inputs.view(-1,28*28) 을 이용해 차원을 변경해 줍니다.

벡터 형태로 나온 출력값을 다시 정사각형 이미지로 변환하기 위해 outputs = outputs.view(-1, 1, 28, 28) 로 원래 이미지 차원으로 변경해 줍니다.

for epoch in range(51):
    running_loss = 0.0
    for data in trainloader:
        inputs = data[0].to(device)
        optimizer.zero_grad()
        # inputs 에 view 를 해주는 이유는 입력 데이터가 이미지 데이터라 채널 차원을 포함하고 있어
        # 채널 차원을 없애주기 위함임
        outputs = model(inputs.view(-1, 28*28))

        # outputs 에 view 를 해주는 이유는 inputs 에서 없애 줬던 채널 정보를 추가한 것임
        outputs = outputs.view(-1, 1, 28, 28)
        loss = criterion(inputs, outputs)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
    cost = running_loss / len(trainloader)
    print("[%d] loss: %.3f"%(epoch+1, cost))

Output: 

[1] loss: 0.083
[2] loss: 0.060
[3] loss: 0.051
[4] loss: 0.044
... 이하 생략 ...

모델 평가

실제로 학습한 모델이 출력해주는 이미지가 실제 이미지와 비슷한지 확인하기 위해 평가 데이터를 이용해 실제 이미지와 모델이 만든 이미지와의 비교를 진행해 보았습니다.

# (1) 테스트 데이터셋 로드
testset = torchvision.datasets.MNIST(root="./data/", download=True, train=False, transform=transforms.ToTensor())
testloader = torch.utils.data.DataLoader(testset, batch_size=10, shuffle=True) # 10개 이미지를 시각화

# (2) 모델을 평가 모드로 설정
#    (Dropout, BatchNorm 등 평가 시에는 불필요한 레이어를 비활성화합니다.)
model.eval()

# (3) 테스트 데이터 한 배치를 가져오기
dataiter = iter(testloader)
images, labels = next(dataiter)
images = images.to(device)

# (4) 모델에 입력을 넣어 결과 얻기
#    torch.no_grad() : 기울기 계산을 하지 않아 메모리 및 연산 효율을 높입니다.
with torch.no_grad():
    # 원본 이미지를 모델에 입력하기 위해 flatten
    flattened_images = images.view(-1, 28*28)
    # 모델의 출력값 (복원된 이미지)
    outputs = model(flattened_images)

# (5) 시각화를 위해 텐서 모양 변경 및 CPU로 이동
# 원본 이미지
images_to_show = images.cpu().numpy()
# 복원된 이미지 (모델 출력을 다시 28x28 이미지 형태로 변경)
outputs_to_show = outputs.view(-1, 1, 28, 28).cpu().numpy()


# (6) Matplotlib을 사용하여 이미지 출력
n_images = 10  # 표시할 이미지 개수

fig, axes = plt.subplots(nrows=2, ncols=n_images, figsize=(15, 3))
plt.gray() # 흑백으로 설정

for i in range(n_images):
    # 원본 이미지 표시 (첫 번째 행)
    ax = axes[0, i]
    ax.imshow(np.squeeze(images_to_show[i]))
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

for i in range(n_images):

    # 복원된 이미지 표시 (두 번째 행)
    ax = axes[1, i]
    ax.imshow(np.squeeze(outputs_to_show[i]))
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

plt.show()

아래 이미지 에서 위는 실제 평가 데이터 이미지이고 아래는 모델이 만든 이미지입니다. 모델이 만든 이미지가 원본 보다는 조금 흐릿하긴 하지만 그래도 완전히 못 알아볼 정도는 아니어서 어느 정도 오토인코더가 동작한다고 볼 수 있습니다.

3. 디노이징 오토인코더

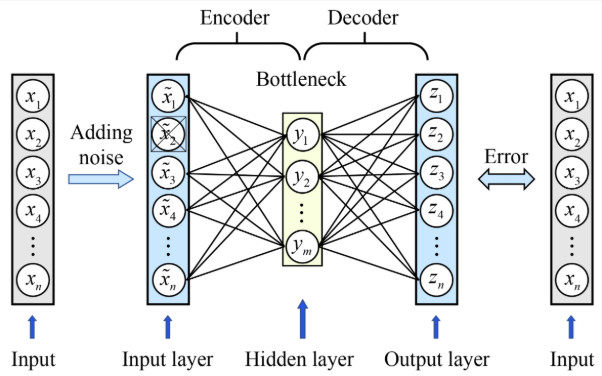
오토인코더의 기본적인 목적은 새로운 데이터를 만드는 것입니다. 따라서 출력 데이터를 입력 데이터에 가까워지도록 학습한다면 기존의 데이터와 매우 유사하여 새로운 데이터를 만드는 의미가 무색해질 수 있습니다. 따라서 입력값에 과적합되지 않도록 입력값에 노이즈를 주입시키거나 신경망에 드롭 아웃을 적용하여 출력 데이터와 노이즈가 없는 원래 입력 데이터를 가지고 손실 함수를 계산합니다. 따라서 노이즈가 있는 이미지를 가지고 노이즈가 없는 이미지와 유사한 데이터를 만드는 구조이기 때문에 이를 디노이징 오토인코더(Denoising autoencoder)라고 합니다. 실제로 이미지 복원이나 노이즈 제거 등에 사용됩니다. 이번 예제에서는 가우시안 노이즈를 주입하여 학습 하는 방법을 구현해보겠습니다.

3.1 모델 코드 설명

노이즈 데이터 만들기

임포트와 데이터, 모델 코드는 이전 오토인코더 코드와 동일합니다. 우선 학습 데이터에서 일정 부분을 추출해 노이즈를 삽입해 보고, 원본 데이터와 비교를 위해 이미지 출력을 진행해 보도록 하겠습니다.

dataiter = iter(trainloader) # 배치 사이즈로 나눠진 데이터를 iteration화 시킴
images, labels = next(dataiter) # 첫 번째 데이터를 가져옴
images = images.to(device)

# 가우시안 노이즈 적용
dirty_images = images + torch.normal(0, 0.5, size=images.size()).to(device)

images_to_show = images.cpu().numpy()
dirty_images_to_show = dirty_images.cpu().numpy()

n_images = 10

fig, axes = plt.subplots(nrows=2, ncols=n_images, figsize=(15, 3))
plt.gray() # 흑백으로 설정

# 원본 이미지와 노이즈가 적용된 이미지 출력
for i in range(n_images):
    ax = axes[0, i]
    ax.imshow(np.squeeze(images_to_show[i]))
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

    ax = axes[1, i]
    ax.imshow(np.squeeze(dirty_images_to_show[i]))
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)

plt.show()

가우시안 노이즈를 주입한 결과 원본 이미지에 예전 TV 송출이 중단된 지지직 거리던 흑백이 추가된 것을 확인할 수 있습니다. 그럼 이렇게 노이즈를 추가한 데이터로 학습을 진행해 보도록 하겠습니다.

학습하기

이전 오토인코더의 학습 부분에 가우시안 노이즈를 주입해주면 됩니다. 노이즈 텐서의 사이즈는 이미지 사이즈와 같아야 하기 때문에 size=inputs.size() 를 입력하고 평균과 표준편차는 임의로 0, 0.5를 넣어주었습니다.

for epoch in range(51):
  running_loss = 0.0
  for data in trainloader:
    inputs = data[0].to(device)
    optimizer.zero_grad()
    dirty_inputs = inputs + torch.normal(0, 0.5, size=inputs.size()).to(device) # 가우시안 노이즈 주입
    outputs = model(inputs.view(-1, 28*28))
    outputs = outputs.view(-1, 1, 28, 28)
    loss = criterion(inputs, outputs)
    loss.backward()
    optimizer.step()
    running_loss += loss.item()
  cost = running_loss / len(trainloader)
  print("[%d] loss: %.3f"%(epoch+1, cost))

이미지 출력은 이전 오토인코더의 이미지 결과를 출력 코드를 그대로 사용하였습니다.

아래 이미지는 디노이징 오토인코더로 학습한 모델을 이용해 이미지를 생성한 결과입니다. 위는 원본 이미지이고, 아래는 모델이 생성한 이미지입니다.

저의 주관으로는 오토인코더 모델보다는 입력에 노이즈를 섞은 디노이징 오토인코더의 결과가 조금 더 좋아보입니다.

4. 합성곱 오토인코더

합성곱 오토인코더(Convolutional autoencoder)는 nn.Linear 대신 합성곱 층 nn.Conv2d 를 사용하는 구조입니다. 따라서 이미지 데이터가 일렬로 펴지지 않고 그대로 들어와 연산이 진행됩니다. 기본적으로 잠재 변수 h 는 일렬 형태인 벡터이기 때문에, 인코더에서 나온 피쳐맵을 일렬로 펴서 h 를 추출하고 다시 h 를 은닉층을 거친 뒤 사각형 모양의 피쳐맵으로 만들어 디코더에 넣어주어야 합니다. 실제 h 를 벡터화하는 방법은 응용 범위가 다양합니다. 그럼 코드로 한 번 알아보도록 하겠습니다.

4.2 모델 코드 설명

피쳐맵을 벡터화하기

Flatten 클래스는 인코더를 거친 후, 정 가운데에 있는 $h$(hidden layer 혹은 Latent Variables) 를 위한 클래스로 피쳐맵 형태에서 일렬로 변환하는 기능을 가진 클래스입니다. 인코더를 거친 피쳐맵의 크기는 (배치 사이즈, 채널 수, 이미지 너비, 이미지 높이)입니다. 따라서 배치 사이즈가 현재 이미지의 개수이므로 벡터가 배치 사이즈 만큼 존재해야 합니다. 즉, x.view(batch_size, -1)를 이용해 각 피쳐 데이터를 일렬로 변환합니다.

# 4D 텐서(Conv용)를 2D 텐서(Linear용)로 펼쳐주는 클래스
# 인코더의 출력값을 입력으로 받는다
class Flatten(torch.nn.Module):
  def forward(self, x):

    """
    입력 x : (Batch_size, Channels, Height, Width)
    출력 : (Batch_size, Channels * Height * Width)
    """
    batch_size = x.shape[0]

    # -1 은 CxHxW 를 자동으로 계산하여 1차원 벡터로 펼치라는 의미
    return x.view(batch_size, -1)

벡터를 사각형 피쳐맵으로 변환하기

Deflatten 클래스는 잠재 변수 h(혹은 hidden_layer) 에서 출력층으로 갈 때 일렬인 벡터를 CNN 에 맞게 피쳐맵으로 바꿔주는 클래스입니다.

feature_size는 잠재 변수 h 를 이용해 구합니다. 잠재 변수 h 의 크기는 (배치사이즈, 채널 수*이미지 너비*이미지 높이)입니다. 따라서 벡터 사이즈는 채널 수*이미지 너비*이미지 높이이고 너비와 높이가 같다면 채널 수*이미지 너비**2가 됩니다. 그래서 이미지 한 변의 길이는 (벡터 사이즈//채널 수)**.5 가 됩니다.

잠재 변수를 이용해 구한 feature_size 를 이용해 피쳐맵의 크기를 (배치 사이즈, 채널 수, 이미지 너비, 이미지 높이) = (s[0], self.k, feature_size, feature_size) 로 변환합니다.

# 2D 텐서 (Linear 출력)를 4D 텐서(ConvTranspose2d 입력)로 복원하는 클래스
class Deflatten(nn.Module):
  def __init__(self, k):
    super(Deflatten, self).__init__()
    # 복원하려는 4D 텐서의 채널 수
    self.k = k # (Autoencoder에서 4xk = 64가 됨)

  def forward(self, x):

    """
    입력 x : (Batch_size, N)
             (Autoencoder 에서는 (Batch_size, 1024))
    """
    s = x.size() # s = [Batch_size, 1024]

    # 복원할 2D 특징 맵(feature map)의 한 변의 크기를 계산
    # s[1] = 1024, self.k = 64
    # 1024 // 64 = 16
    # 16의 제곱근 = 4
    # 즉, 1024개의 1D 벡터를 (64, 4, 4)의 3D 텐서로 복원하겠다는 의미
    feature_size = int((s[1]//self.k)**.5)
    return x.view(s[0], self.k, feature_size, feature_size)

모델 구축하기

모델의 decoder 를 보면 nn.Conv2d 대신 nn.ConvTranspose2d 를 사용합니다. 그 이유는 크기가 작은 입력값을 크기가 큰 입력값으로 만들기 위함입니다. nn.ConvTranspose2d 는 입력 성분(Conv의 결과)을 출력 성분(Conv의 입력)으로 미분하여 그 값을 입력 벡터와 곱해 출력 벡터를 산출하고 그 결과 벡터를 행렬 형태로 변환하는 연산입니다. 이렇게 말하면 잘 이해가 되질 않습니다.

쉽게 설명하자면 Conv2d 는 큰 이미지를 작은 특징 맵으로 요약하는 과정입니다. 마치 넓은 사진에서 돋보기(커널)를 움직이며 중요한 특징(윤곽선, 질감 등)만 찾아 작은 스케치북에 옮겨 그리는 것과 같으며, 이러한 과정을 진행하면 이미지는 작은 피쳐맵으로 압축되게 됩니다. 하지만 현재 우리가 알아보고 있는 합성곱 오토인코더의 디코더는 인코더에서 Conv2d 를 통해 압축된 피쳐맵을 다시 원본 이미지로 되돌려야 합니다. 그래서 Conv2d 반대로 동작하는 ConvTranspose2d 를 사용하는 것입니다. ConvTranspose2d 는 작은 특징 맵(요약본)을 가지고 원래의 큰 이미지로 확장/복원 할 수 있습니다. 업 샘플링(Upsampling) 컨볼루션이라고도 불립니다. ConvTranspose2d 를 이용해 도출되는 확장/복원된 피쳐맵의 크기는 다음 식에 의해 크기를 산출할 수 있습니다.

(출력값의 크기) = (입력값의 크기-1)x(보폭)-2*(패딩)+(필터의 크기) + (출력값 패딩)

class Autoencoder(nn.Module):
  def __init__(self):
    super(Autoencoder, self).__init__()
    
    # 기본 채널 수
    k = 16

    # Encoder
    # 이미지 (28x28)를 10차원의 잠재 벡터(latent vector)로 압축
    # 입력 : (Batch_size, 1, 28, 28)
    self.encoder = nn.Sequential(
        # (1, 28, 28) -> (k=16, 13, 13)
        # Out = (In = Kernel + 2*Pad) / Stride + 1
        # = (28 - 3) / 2 + 1 = 12.5 + 1 = 13 (floor)
        nn.Conv2d(1, k, 3, stride=2), nn.ReLU(),

        # (16, 13, 13) -> (2k=32, 6, 6)
        # Out = (13 - 3) / 2 +1 = 5 + 1 = 6
        nn.Conv2d(k, 2*k, 3, stride=2), nn.ReLU(),

        # (32, 6, 6) - > (4k=64, 4, 4)
        # Out = (6 - 3) / 1 + 1 = 3 + 1 = 4
        nn.Conv2d(2*k, 4*k, 3, stride=1), nn.ReLU(),

        # (Batch_size, 64, 4, 4) -> (Batch_size, 64*4*4) = (Batch_size, 1024)
        Flatten(), nn.Linear(1024, 10), nn.ReLU())

    # Decoder
    # 10차원의 잠재 벡터를 다시 이미지(28x28)로 복원
    # 입력 : (Batch_size, 10)
    self.decoder = nn.Sequential(
        # (Batch_size, 10) -> (Batch_size, 1024)
        nn.Linear(10, 1024), nn.ReLU(),

        # (Batch_size, 1024) -> (Batch_size, 4k=64, 4, 4)
        Deflatten(4*k),

        # (64, 4, 4) -> (2k=32, 6, 6)
        # Out = (In - 1)*Stride - 2*Pad + Kernel + Out_Pad
        # = (4 - 1)*1 + 3 = 3 + 3 = 6
        nn.ConvTranspose2d(4*k, 2*k, 3, stride=1), nn.ReLU(),

        # (32, 6, 6) -> (k=16, 13, 13)
        # Out = (6 - 1)*2 + 3 = 10 + 3 = 13
        nn.ConvTranspose2d(2*k, k, 3, stride=2), nn.ReLU(),

        # (16, 13, 13) -> (1, 28, 28)
        # Out = (13 - 1)*2 + 3 = 24 + 3 = 27
        # -> 크기가 28이 안맞으므로 output_padding=1 추가
        # Out = (13 - 1)*2 + 3 + 1 = 24 + 3 + 1 = 28
        nn.ConvTranspose2d(k, 1, 3, stride=2, output_padding=1), nn.Sigmoid())

  def forward(self, x):

    # x -> encoder -> encoded(잠재 벡터)
    encoded = self.encoder(x)

    # encoded -> decoder -> decoded (복원된 이미지)
    decoded = self.decoder(encoded)
    return decoded

모델, 손실 함수, 최적화 기법 정의하기

model = Autoencoder().to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)

학습하기

for epoch in range(51):
  running_loss = 0.0
  for data in trainloader:
    inputs = data[0].to(device)
    optimizer.zero_grad()
    outputs = model(inputs)
    loss = criterion(outputs, inputs)
    loss.backward()
    optimizer.step()
    running_loss += loss.item()

  cost = running_loss /len(trainloader)
  if epoch % 10 == 0:
    print("[%d] loss: %.3f"%(epoch+1, cost))

모델을 이용한 이미지 출력하기

test_dataset = torchvision.datasets.MNIST(root="./data/", download=True, train=False, transform=transforms.ToTensor())
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=10, shuffle=True) # 10개의 이미지를 시각화합니다.

model.eval()

dataiter = iter(test_loader)
images, labels = next(dataiter)
images = images.to(device)

with torch.no_grad():
    outputs = model(images)

original_images = images.cpu().numpy()
reconstructed_images = outputs.cpu().numpy()

n = 10  # 표시할 이미지 개수
plt.figure(figsize=(20, 4))
print("Top row: Original Images, Bottom row: Reconstructed Images")

for i in range(n):
    # 원본 이미지 표시
    ax = plt.subplot(2, n, i + 1)
    plt.imshow(np.squeeze(original_images[i]), cmap='gray')
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    if i == n // 2:
        ax.set_title('Original Images')

    # 복원된 이미지 표시
    ax = plt.subplot(2, n, i + 1 + n)
    plt.imshow(np.squeeze(reconstructed_images[i]), cmap='gray')
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    if i == n // 2:
        ax.set_title('Reconstructed Images')
plt.show()

5. 생성적 적대 신경망(GAN)

생성적 적대 신경망(Generative adversarial network, GAN)은 아이디어 자체만으로 매우 가치있는 모델로 평가 받고 있습니다. 실제로 얼굴 변환, 생성, 음성 변조, 그림 스타일 변환, 사진 복원 등 다양한 기술로 응용되고 있습니다. 기본적으로 생성적 적대 신경망은 진짜 같은 가짜 데이터를 만들어 내는 기술입니다.

GAN 모델은 가짜 이미지는 만드는 생성자(Generator)와 진짜 이미지와 가짜 이미지를 구별하는 구별자(Discriminator)로 구성되어 있습니다. 따라서 구별자는 진짜와 가짜 판별을 0과 1로 구분하게 됩니다. 이 때 생성자 입장에서는 구별자가 구분을 못하는 이미지를 만들도록 해야하며, 구별자는 진위 여부를 잘 가리도록 모델이 만들어져야합니다. 좀 더 쉽게 GAN 의 작동 원리를 표현하자면 경찰과 위조지폐범의 경쟁 관계로 비유할 수 있습니다. 생성자는 위조지폐범, 판별자는 경찰로 비유하는 것입니다. 이를 손실 함수로써 수식으로 정의하면 다음과 같습니다.

\[\min_G \max_D V(D, G) = \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [\log(1 - D(G(z)))]\]

수식의 목표는 구별자와 생성자가 서로 경쟁하도록 해서 구별자는 진짜 데이터와 생성자가 만든 가짜 데이터를 잘 판별하도록 학습하는 것이고, 생성자는 구별자가 구별할 수 없게 생성자가 생성하는 데이터를 진짜 데이터에 가깝게 만들도록 학습하는 것입니다. 여기서 설명을 위해 구별자를 경찰, 생성자를 위조지폐범으로 비유해서 설명을 진행하도록 하겠습니다. 경찰인 구별자의 목표는 진짜 데이터(x)와 가짜 데이터(G(z))를 최대한 잘 구별해는 것입니다. 즉 수식의 값(V)을 최대화하는 것이 목표입니다. 위조지폐범인 생성자의 목표는 경찰인 구별자를 완벽하게 속여서, 자신이 만든 가짜 데이터가 진짜처럼 보이게 만드는 것입니다. 즉, 경찰이 구별을 못하게 만들어야 하므로 수식의 값(V)을 최소화하는 것이 목표입니다.

그렇다면 수식을 분해해서 보도록 하겠습니다. $\max_{D}$ 는 경찰(D)이 똑똑해지는 과정입니다. 경찰은 V 라는 점수를 최대한 높이는 방향으로 훈련합니다.

$ \mathbb{E}_{x \sim P{data}(x)}[\log D(x)] $ 는 진짜 데이터에 대해서는 경찰(D)이 진짜 데이터에 대해서는 진짜일 확률을 높게 만들고 싶다는 의미를 가집니다. 세세하게 하나 하나 뜯어보자면 $D(x)$ 는 경찰(D)이 진짜 데이터(x)를 보고 “진짜”라고 판단할 확률입니다. 경찰의 목표는 진짜를 보고 진짜라고 확신하는 것입니다. 즉 $D(x)$를 1에 가깝게 만드는 것입니다. $D(x)$가 1에 가까워지면 $\log D(x)$ 의 값은 0이 되므로 진짜 데이터를 진짜로 잘 판별할 수록 손실 값은 작아지게 되며, 경찰은 높은 점수를 받게됩니다.

$\mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]$ 는 가짜 데이터($G(z)$)에 대해서 경찰이 가짜일 확률을 높게 만들고 싶다는 의미를 가집니다. $G(z)$ 는 위조지폐범(G)이 랜덤 노이즈(z)로 만든 가짜 데이터입니다. $D(G(z))$ 는 경찰(D)이 가짜 데이터($G(z)$)를 보고 “진짜”라고 판단할 확률입니다. 경찰의 목표는 가짜를 가짜라고 확신하는 것이므로 $D(G(z))$ 값을 0에 가깝게 만드는 것입니다. $D(G(z))$가 0에 가까워지면 $\log(1 - D(G(z)))$ 값은 0에 가까워지며 커집니다.

$\min_{G}$ 는 위조지폐범(G)이 똑똑해지는 과정입니다. 위조지폐범은 경찰이 점수를 최대한 못 얻도록, 즉 V 점수를 가장 낮추는 방향으로 학습됩니다. 위조지폐범은 첫 번째 항 $\log D(x)$ 에는 영향을 줄 수 없습니다. 진짜 데이터는 위조지폐범이 건드릴 수 없기 때문입니다. 위조지폐범은 두 번째 항 $\log(1 - D(G(z)))$ 값을 최소화해야 합니다. 이 값을 최소화하려면 $D(G(z))$ 가 1에 가까워져야 합니다. 즉, 경찰이 자신이 만든 가짜 데이터를 보고 “진짜”라고 판단하게 만들어야 합니다.

5.1 Vanilla GAN

라이브러리 불러오기

격자 형태의 이미지를 만들게 하는 make_grid와 gif 파일을 만들기 위한 imageio 를 추가적으로 불러옵니다.

import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import transforms
from torch.utils.data import DataLoader
from torchvision.datasets import FashionMNIST
from torchvision.utils import make_grid
import imageio
import numpy as np
from matplotlib import pyplot as plt

패션 아이템 데이터 불러오기

티셔츠, 바지, 풀오버, 드레스, 코트, 샌들, 셔츠, 스니커즈, 가방, 앵클부츠로 구성된 FashionMNIST 데이터를 불러옵니다.

transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))])
trainset = FashionMNIST(root="./data", train=True, download=True, transform=transform)
trainloader = DataLoader(trainset, batch_size=100, shuffle=True)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

불러온 데이터를 출력해보면 다음과 같습니다.

생성자 구축하기

생성자는 잠재 변수로부터 784(28x28) 크기인 벡터를 생성합니다. 따라서 잠재 변수의 크기를 임의로 정하고 출력 크기는 이미지를 일렬로 편 크기인 784로 정의합니다.

Vanilla GAN 에서는 nn.Linear 을 이용하여 모델을 구축하며, 활성 함수로는 nn.LeakyReLU 를 사용합니다. ReLU 는 입력값이 0보다 작으면 0으로 값을 바꿔줍니다. 따라서 음수 구간에서 미분을 할 경우 0이 나옵니다. 이 때 기울기 사라짐 방지를 위해 음수 구간에 양의 기울기를 주어 값을 계산하는 LeakyReLU(0.2) 로 대체를 합니다. 0.2 는 음수 구간의 그래프가 y=0.2x 라는 의미로 직선의 기울기를 나타냅니다.

정의된 MLP 를 거치고 784 크기의 벡터를 크기가 28x28 인 흑백 이미지로 변경하여 새로운 이미지를 생성합니다.

class Generator(nn.Module):
  def __init__(self):
    super(Generator, self).__init__()

    # 입력으로 받아오는 잠재 벡터의 크기
    self.n_features = 128

    # 최종 출력 벡터의 크기
    # 사용하는 입력 이미지의 크기가 28x28 이므로 784
    self.n_out = 784
    self.linear = nn.Sequential(
        nn.Linear(self.n_features, 256),
        nn.LeakyReLU(0.2),
        nn.Linear(256, 512),
        nn.LeakyReLU(0.2),
        nn.Linear(512, 1024),
        nn.LeakyReLU(0.2),
        nn.Linear(1024, self.n_out),
        nn.Tanh())

  def forward(self, x):
    x = self.linear(x)

    # 모델의 출력을 이미지로 바꾸기 위해 view 사용
    x = x.view(-1, 1, 28, 28)
    return x

구별자 구축하기

입력의 크기는 이미지를 일렬로 편 크기를 입력합니다.

출력값은 진위여부를 판단하기 위해 하나의 숫자로 정의합니다.

class Discriminator(nn.Module):
  def __init__(self):
    super(Discriminator, self).__init__()
    self.n_in = 784
    self.n_out = 1
    self.linear = nn.Sequential(
        nn.Linear(self.n_in, 1024),
        nn.LeakyReLU(0.2),
        nn.Dropout(0.3),
        nn.Linear(1024, 512),
        nn.LeakyReLU(0.2),
        nn.Dropout(0.3),
        nn.Linear(512, 256),
        nn.LeakyReLU(0.2),
        nn.Dropout(0.3),
        nn.Linear(256, self.n_out),

        # Sigmoid 함수를 이용해 출력 벡터의 값을 0~1 사이의 값으로 만들어줌
        nn.Sigmoid())

  def forward(self, x):
    x = x.view(-1, 784)
    x = self.linear(x)
    return x

모델 정의하기

generator = Generator().to(device)
discriminator = Discriminator().to(device)

손실 함수 및 최적화 기법 정의하기

생성자 변수 최적화를 위해 Adam 을 정의합니다.

구별자 변수 최적화를 위해 Adam 을 별도로 정의합니다.

학습 동안 생성자와 구별자의 손실값과 샘플 이미지 저장을 위해 빈 리스트를 만듭니다.

손실 함수는 이진 크로스 엔트로피 함수를 사용합니다.

g_optim = optim.Adam(generator.parameters(), lr=2e-4)
d_optim = optim.Adam(discriminator.parameters(), lr=2e-4)
g_losses = []
d_losses = []
images = []
criterion = nn.BCELoss()

잠재 변수 및 라벨 정의하기

noise 함수는 기본적으로 크기가 128인 잠재 변수 n 개를 무작위로 생성하는 함수입니다.

label_ones 와 label_zeros 함수는 1과 0 라벨을 만들어주는 함수인데, 이 함수가 필요한 이유는 손실 함수에서 이미지의 진위 여부에 대한 계산을 하게 될 때 실제 이미지의 클래스를 사용하지 않고, 진짜 데이터는 1, 생성자로부터 만들어진 이미지의 라벨은 0이라고 정의하기 위함입니다.

# 노이즈 데이터를 만들기 위한 함수
def noise(n, n_features=128):
  data = torch.randn(n, n_features)
  return data.to(device)

# 실제 이미지 데이터에 1로 라벨을 붙여주기 위한 함수
def label_ones(size):
  data = torch.ones(size, 1)
  return data.to(device)

# 생성자가 생성한 이미지 데이터에 0으로 라벨을 붙여 주기 위한 함수
def label_zeros(size):
  data = torch.zeros(size, 1)
  return data.to(device)

구별자 학습 함수 정의하기

입력 파라메터로 최적화 함수, 진짜 이미지, 가짜 이미지를 받아옵니다.

n 은 각 이미지 진위 라벨을 할당하기 위한 이미지의 개수입니다.

prediction_real 은 구별자 모델을 이용해 진짜 이미지 판별을 진행합니다.

이미지 수 만큼 ‘1’라벨을 넣어 구별자 손실 함수를 계산합니다.

가짜 이미지도 똑같이 가짜 이미지를 판별하고 이미지 수 만큼 0라벨을 넣어 손실 함수를 계산합니다.

두 손실 함수의 합을 최종 손실 함수로 사용하여 구별자를 업데이트 합니다.

# 구별자 학습 함수
def train_discriminator(optimizer, real_data, fake_data):
  n = real_data.size(0)
  optimizer.zero_grad()

  # 모델에 실제 데이터를 입력으로 넣어 출력 벡터를 얻음
  prediction_real = discriminator(real_data)

  # 실제 이미지로 얻은 출력 벡터와 실제 라벨을 비교 이 때 라벨은 실제 데이터 이므로 모두 1임
  d_loss = criterion(prediction_real, label_ones(n))

  # 직접 만든 노이즈 데이터를 입력으로 넣어 출력 벡터를 얻음
  prediction_fake = discriminator(fake_data)

  # 노이즈 데이터의 출력 벡터와 라벨을 비교 이때 라벨은 노이즈 데이터 이므로 모두 0임
  g_loss = criterion(prediction_fake, label_zeros(n))

  # 실제 이미지와 노이즈 이미지로 만든 벡터의 손실값을 합침
  loss = d_loss + g_loss

  # loss 값을d_optim 에 반영
  loss.backward()
  optimizer.step()
  return loss.item()

생성자 학습 함수 정의하기

입력 파라메터로 최적화 함수, 가짜 이미지를 받아옵니다.

가짜 이미지를 구별자에 넣어 판별합니다. 그리고 생성자 입장에서는 구별자가 진짜 이미지라고 판단하도록 업데이트가 되어야 하므로 0라벨이 아닌 1라벨을 넣어 손실 함수를 계산하게 합니다. 이러한 방식으로 min max 형태의 손실 함수를 직접 구현하지 않고 최적화를 수행할 수 있습니다.

# 생성자 학습 함수
def train_generator(optimizer, fake_data):
  n = fake_data.size(0)
  optimizer.zero_grad()

  # 노이즈 데이터를 구별자에 넣어 출력 벡터를 얻음
  prediction = discriminator(fake_data)

  # 생성자는 구별자가 진짜 데이터와 노이즈 데이터를 구분하지 못하게 학습을 진행해야 하므로
  # 노이즈 데이터의 출력 벡터가 진짜 데이터인 라벨 1이 되도록 학습을 해야 함
  # 그러므로 사용하는 라벨은 1임
  loss = criterion(prediction, label_ones(n))

  # loss 값을 g_optim 에 반영
  loss.backward()
  optimizer.step()
  return loss.item()

모델 학습하기

test_noise = noise(64) 는 검증을 위한 무작위 변수 64개를 생성합니다.

test_noise = noise(64)
l = len(trainloader)

for epoch in range(151):
  g_loss = 0.0
  d_loss = 0.0

  for data in trainloader:
    imgs, _ = data
    n = len(imgs)
    fake_data = generator(noise(n)).detach()
    real_data = imgs.to(device)
    d_loss += train_discriminator(d_optim, real_data, fake_data)

    fake_data = generator(noise(n))
    g_loss += train_generator(g_optim, fake_data)


  img = generator(test_noise).detach().cpu()
  img = make_grid(img)
  images.append(img)
  g_losses.append(g_loss/l)
  d_losses.append(d_loss/l)
  if epoch % 10 == 0:
    print("Epoch {}: g_loss : {:.3f} d_loss:{:.3f}\r".format(epoch, g_loss/l, d_loss/l))

모델 저장하기

torch.save(discriminator.state_dict(),"/content/drive/MyDrive/pytorch/models/fmnist_disc.pth")
torch.save(generator.state_dict(), "/content/drive/MyDrive/pytorch/models/fmnist_gner.pth")

검증 이미지 변화를 위한 gif 파일로 저장하기

to_image 는 생성자를 통해 생성된 이미지를 저장 형식에 맞추기 위해 ToPILImage() 를 이용해 타입과 크기(3, 242, 242) 를 변환할 수 있도록 하기 위한 변수입니다. images 리스트에 저장되는 생성자가 생성한 이미지는 격자 형태로 만들어진 이미지들의 모임이며 크기가 (3, 242, 242)입니다.

이미지를 넘파이 배열로 변경하여 gif 파일로 만듭니다.

to_image = transforms.ToPILImage()
imgs = [np.array(to_image(i)) for i in images]
imageio.mimsave("/content/drive/MyDrive/pytorch/models/fashion_items.gif", imgs)

아래는 생성자가 생성한 이미지로 만든 gif 입니다.

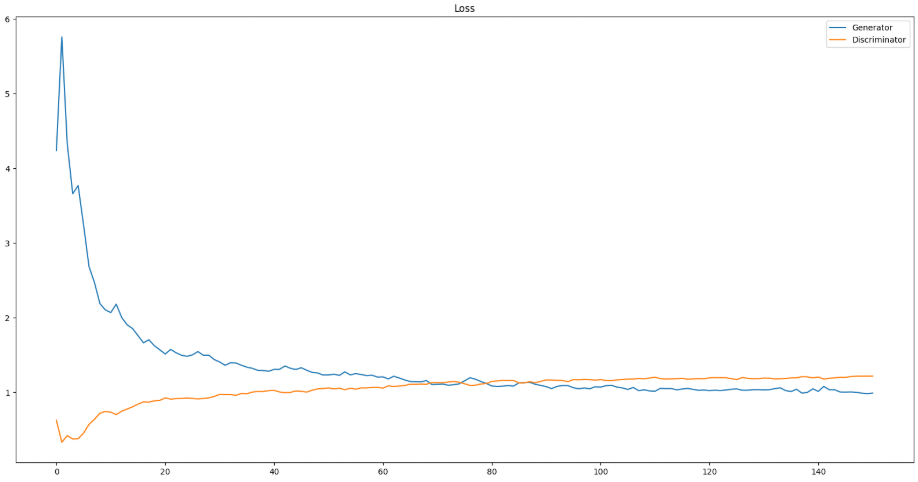
손실 함수값 그래프 그리기

plt.figure(figsize=(20,10))
plt.plot(g_losses)
plt.plot(d_losses)
plt.legend(['Generator', 'Discriminator'])
plt.title("Loss")
plt.savefig('gan_loss.png')

5.2 Deep Convolutional GAN(DCGAN)

DCGAN 은 GAN 구조를 합성곱 층으로 구성한 모델입니다. 합성곱 신경망은 다층 퍼셉트론보다 이미지 처리에 매우 유리한 네트워크로 알려져 있습니다. 실제 다층 퍼셉트론으로 구성된 GAN 보다 DCGAN 을 통해 조금 더 선명한 이미지를 생성할 수 있습니다. 이번 예제는 Vanilla GAN 에서 합성곱 층으로 변경하여 진행합니다.

생성자 구축하기

입력은 크기가 128인 잠재 변수를 가지고 채널이 128개인 1x1 크기의 이미지를 입력으로 받습니다.

생성자는 일렬 벡터인 노이즈로부터 28x28 이미지 한 장을 얻기 위해 nn.ConvTranspose2d 를 사용합니다.

class Generator(nn.Module):

    """
    128차원의 잠재 벡터(noise)를 입력받아
    (1, 28, 28) 크기의 가짜 이미지를 생성하는 모델
    """

    def __init__(self):
        super(Generator, self).__init__()
        
        # 입력 잠재 벡터(noise)의 차원
        self.n_features = 128

        # ConvTranspose2d 연산을 순차적으로 수행
        # (Input: 128, 1, 1) -> (Output : 1, 28, 28)
        self.conv = nn.Sequential(

            # ConvTranspose2d(입력 채널, 출력 채널, 커널, 스트라이드, 패딩, bias)

            # Input : (128, 1, 1)
            # Out = (In-1)*Stride + Kernel = (1-1)*1 + 3 = 3
            # Output: (256, 3, 3)
            nn.ConvTranspose2d(self.n_features, 256, 3, 1, bias=False), nn.ReLU(True),

            # Input : (256, 3, 3)
            # Out = (3*1)*2 + 3 = 4 + 3 = 7
            # Output : (128, 7, 7)
            nn.ConvTranspose2d(256, 128, 3, 2, bias=False), nn.ReLU(True),

            # Input : (128, 7, 7)
            # Out = (7-1)*2 + 3 = 12 + 3 = 15
            # Output : (64, 15, 15)
            nn.ConvTranspose2d(128, 64, 3, 2, bias=False), nn.ReLU(True),

            # Input : (64, 15, 15)
            # Out : (In-1)*Stride - 2*Pad + Kernel = (15-1)*2 - 2*1 + 2 = 28-2+2 = 28
            nn.ConvTranspose2d(64, 1, 2, 2, 1, bias=False), 
            
            # 최종 출력 픽셀 값을 -1 ~ 1 사이로 조정
            nn.Tanh()
        )

    def forward(self, x):

        # 잠재 벡터를 (B, 128, 1, 1) 4D 텐서로 변환
        x = x.view(-1, self.n_features, 1, 1)

        # ConvTranspose 연산 수행
        x = self.conv(x)

        # (B, 1, 28, 28) 크기의 생성된 이미지 반환
        return x

구별자 구축하기

진위 여부를 구별하기 위해 합성곱 신경망을 적용합니다. 일반적으로 합성곱 층의 필터는 특징을 추출하는 역할을 하기 때문에 Dropout 을 사용하지 않습니다. 하지만 이번 예시에서는 구별자에 Dropout 을 적용하여 생성자보다 불리한 조건을 가지게 합니다.

class Discriminator(nn.Module):
    """
    (1, 28, 28) 크기의 이미지(진자 또는 가짜)를 입력받아
    이 이미지가 "진짜"일 확률 (0~1 사이의 값)을 출력하는 모델
    """
    def __init__(self):
        super(Discriminator, self).__init__()

        # Conv2d 연산을 순차적으로 수행
        # (Input: 1, 28, 28) -> (Output: 1, 1, 1)
        self.conv = nn.Sequential(
            
            # Conv2d(입력 채널, 출력 채널, 커널, 스트라이드, 패딩, bias)
            
            # Input : (1, 28, 28)
            # Output = (In + 2*Pad - Kernel) / Stride + 1 = (28 + 2*1 - 3) / 2 + 1 = 27/2 + 1 = 13.5 + 1 = 14
            # Output: (128, 14, 14)
            nn.Conv2d(1, 128, 3, 2, 1, bias=False),
            nn.LeakyReLU(0.2),
            nn.Dropout(0.5),

            # Input: (128, 14, 14)
            # Out = (14 + 2*1 - 3) / 2 + 1 = 13/2 + 1 = 6.5 + 1 = 7
            # Output: (256, 7, 7)
            nn.Conv2d(128, 256, 3, 2, 1, bias=False),
            nn.LeakyReLU(0.2),
            nn.Dropout(0.5),

            # Input: (256, 7, 7)
            # Out = (7 + 2*1 - 3) / 2 + 1 = 6/2 + 1 = 3 + 1 = 4
            # Output: (256, 4, 4)
            nn.Conv2d(256, 256, 3, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            nn.Dropout(0.5),

            # Input: (256, 4, 4)
            # Padding=0 (default), Stride=2, Kernel=3
            # Out = (4 - 3) / 2 + 1 = 1/2 + 1 = 0.5 + 1 = 1
            # (참고: 코드의 '3, 2' 뒤에 패딩이 없으므로 기본값 0)
            # Output : (1, 1, 1) -> 최종 판별값
            nn.Conv2d(256, 1, 3, 2, bias=False),

            # 최종 출력(logit)을 0~1 사이의 확률값으로 변환
            nn.Sigmoid()
        )

    def forward(self, x):
        """
        x: (Batch_size, 1, 28, 28) 크기의 이미지 텐서
        """

        # (B, 1, 28, 28) -> (B, 1, 1, 1)
        x = self.conv(x)

        # 4D 텐서를 2D 텐서 (B, 1)로 변환
        # (B, 1, 1, 1) -> (B, 1)
        # BCELoss 같은 손실 함수가 (B, 1) 형태의 입력을 기대하기 때문
        return x.view(-1, 1)

손실 함수값 그래프

DCGAN 모델은 Vanilla GAN 과 달리 loss 값이 크게 감소했다가 들쭉 날쭉 하는 모습을 볼 수 있습니다. GAN 모델의 특성상 학습이 잘 되지 않아 발생하는 현상입니다.

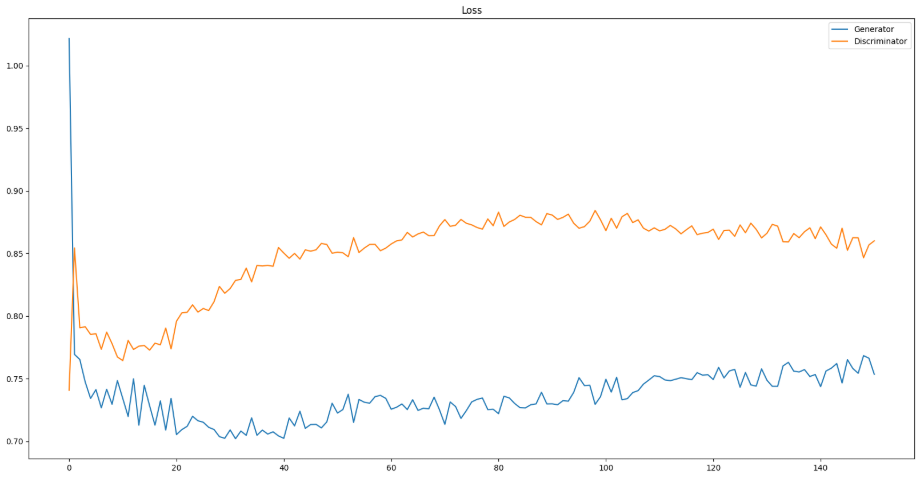
Vanilla GAN 과 DCGAN 결과 비교

이번 DCGAN 모델이 학습이 잘 되지 않아 GAN 의 결과보다 더 흐릿한 것을 볼 수 있습니다. GAN 모델들의 경우 학습에 시간 소요가 크기 때문에 다음에 기회가 된다면 DCGAN 도 제대로 학습 한 뒤에 다시 비교해보고, 포스트를 수정하도록 하겠습니다.

6. 이미지 스타일 변이

이미지 스타일 변이(Image style transfer)는 한 장의 스타일 이미지와 한 장의 내용 이미지를 가지고 새로운 스타일의 이미지를 만드는 비지도 학습 방법입니다. 따라서 우리는 임의의 결과 이미지를 만들고 우리가 원하는 그림이 나올 수 있도록 결과 이미지를 업데이트합니다. 지금까지 배웠던 방법들이 모델들을 최적화했다면, 스타일 변이는 결과 이미지를 최적화하는 작업을 수행합니다. 즉, 모델은 학습된 모델을 사용하고 최적화를 진행하지 않습니다.

6.2 모델 코드 설명

라이브러리 불러오기

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from PIL import Image
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
import torchvision.models as models

모델 불러오기

이미지의 유의미한 특성을 추출하기 위해 사전 훈련된 모델 중 피쳐 추출 부분(합성곱 층)을 불러옵니다. 또한 모델에 대해 업데이트를 하고 피쳐 추출 용도로 사용하기 때문에 eval() 을 활성화 합니다.

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
cnn = models.vgg19(pretrained=True).features.to(device).eval()

내용 손실 함수 정의하기

업데이트를 하고자 하는 내용 이미지(input)의 피쳐맵과 원래의 내용 이미지(self.target)의 피쳐맵의 손실을 계산하기 위해 MSE 손실 함수를 사용합니다.

# 생성된 이미지와 원본 '내용' 이미지의 차이를 계산
class ContentLoss(nn.Module):
    def __init__(self, target,):
        """
        target: 원본 "내용" 이미지의 특정 VGG 레이어에서 나온 특징맵
        """
        super(ContentLoss, self).__init__()

        # self.target 에 detach() 합니다.
        # target 은 고정된 값이며, 이 텐서에 대한 gradient 가 계산되는 것을 방지합니다 (메모리 절약 및 오류 방지)
        self.target = target.detach()

    def forward(self, input):

        """
        input: "생성 중인 이미지"가 동일한 VGG 레이어를 통과해서 나온 "특징 맵"
        """

        # 생성 중인 이미지의 특징 맵(input)과
        # 원본 내용 이미지의 특징 맵(self.target) 사이의
        # 평균 제곱 오차(MSE)를 계산합니다.
        self.loss = F.mse_loss(input, self.target)

        # 이 모듈은 '손실' 계산을 'self.loss'에 저장하는 것을 "부수 효과(side-effect)"로 수행합니다.
        # 모듈 자체는 'input'을 그대로 반환하여,
        # nn.Sequential 모델에서 다음 레이어로 텐서가
        # 계속 전달될 수 있도록 합니다.
        return input

스타일 손실 함수 정의하기

스타일 손실 함수는 내용 손실 함수와는 다르게 각 피쳐맵의 유사도를 비교하기 위해 피쳐맵의 Gram_matrix 를 구한 결과 값을 사용하여 MSE 손실 함수를 계산합니다.

크기가 (c)x(d) 인 이미지를 일렬 벡터로 (배치 크기 a)x(채널 수 b) 개 만큼 만듭니다. 즉 features 는 벡터들의 모임인 2차원 텐서가 됩니다.

feature 를 F 라 하면 F 의 전체 텐서와 F 의 행렬 곱을 수행합니다. 즉 각 벡터들의 내적을 계산하여 유사도를 정량적으로 표현할 수 있습니다.

마지막으로 전체 크기로 나누어 값을 반환합니다.

# 스타일 손실을 계산하기 위한 핵심 함수
def gram_matrix(input):

    """
    특징 맵을 입력받아 그램 행렬을 계산합니다.
    그램 행렬은 각 채널(특징) 간의 '상관관계(correlation)'를 나타내며,
    이것이 곧 이미지의 '스타일'이라고 간주됩니다.

    input: (B, C, H, W) 크기의 4D 텐서 (특징 맵)
    (B=Batch_size, C=Channels, H=Height, W=Width)
    """
    a, b, c, d = input.size() # a = 배치, b=채널 수, c=높이, d=너비

    # (B, C, H, W) -> (B*C, H*W)로 텐서의 모양을 변경
    # 여기서는 (C, H*W)가 됩니다.
    features = input.view(a * b, c * d)

    # (C, H*W) 와 (H*W, C) [전치(transpose)를] 행렬 곱합니다.
    # G의 크기: (C, C)
    # G[i, j]는 i번째 특징 맵과 j번째 특징 맵의 내적(dot product)으로,
    # 두 특징이 이미지에서 얼마나 '함께' 나타나는지를 의미합니다.
    G = torch.mm(features, features.t())

    # 정규화(Normalization)
    # 그램 행렬의 값을 전체 요소 수(a*b*c*d)로 나누어,
    # 특징 맵의 크기나 채널 수에 상관없이 일관된 스케일의
    # 스타일 손실을 얻도록 합니다.
    return G.div(a * b * c * d)

스타일 이미지(self.target)와 업데이트할 이미지(input)의 각 피쳐맵의 Gram_matrix 를 각각 구합니다. 그리고 Gram_matrix 를 사용하여 MSE 를 계산합니다.

# 생성된 이미지와 원본 '스타일' 이미지의 차이를 계산
class StyleLoss(nn.Module):
    def __init__(self, target_feature):

        """
        target_feature: 원본 '스타일' 이미지의 특정 VGG 레이어에서 나온 '특징 맵'
        """
        super(StyleLoss, self).__init__()

        # 1. 원본 스타일 이미지의 특징 맵으로 '그램 행렬'을 계산
        # 2. detach() 하여 이 타겟 그램 행렬이 학습되지 않도록 고정
        self.target = gram_matrix(target_feature).detach()

    def forward(self, input):

        """
        input: '생성 중인 이미지'가 동일한 VGG 레이어를 통과해서 나온 '특징 맵'
        """

        # 생성 중인 이미지의 특징 맵으로 '그램 행렬'을 계산
        G = gram_matrix(input)

        # 생성 중인 이미지의 그램 행렬(G)과 원본 스타일의 그램 행렬(self.target) 사이의 MSE를 계산
        self.loss = F.mse_loss(G, self.target)

        # ContentLoss와 마찬가지로, input을 그대로 반환(Pass-through)
        return input

정규화 함수 정의하기

평균과 표준편차를 정의합니다. 입력으로 들어오는 이미지에 대해 정규화를 진행합니다.

# VGG 모델에 입력하기 전 이미지를 정규화하는 모듈
class Normalization(nn.Module):
    def __init__(self, mean, std):

        """
        mean, std: ImageNet 학습 시 사용된 평균과 표준편차 (e.g., [0.48, 0.456, 0.406])
        """
        super(Normalization, self).__init__()

        # (3) -> (3, 1, 1)로 모양을 변경합니다.
        # (B, 3, H, W) 크기의 이미지 텐서에 브로드캐스팅(broadcasting)으로 연산(+, /)이 가능하도록 하기 위함
        self.mean = mean.view(-1, 1, 1)
        self.std = std.view(-1, 1, 1)

    def forward(self, img):
        # (img-mean)/std 정규화 수행
        return (img - self.mean) / self.std

모델 재정의하기

스타일 변환을 위해 모델 중간의 피쳐맵의 결과들을 활용해 손실 함수를 계산합니다. 따라서 어느 부분의 정보를 사용할 것인지를 정의해야 합니다.

content_layers = ['conv_4'] 내용 손실 함수는 VGG19 모델의 4번째 합성곱 층의 피쳐맵을 사용하여 계산합니다.

style_layers = ['conv_1', 'conv_2', 'conv_3', 'conv_4', 'conv_5'] 스타일 손실 함수는 1번째부터 5번째 합성곱 층의 피쳐맵을 사용합니다. 이 때 스타일 손실 함수는 학습 시 각 층의 손실 함수들의 합으로 정의합니다.

normalization_mean, normalization_std 는 정규화에 필요한 표준편차를 정의합니다.

첫 번째 루프문 for layer in cnn.children(): 는 VGG19 모델의 층을 하나씩 불러옵니다. 그리고 만약 층이 합성곱층이면 i에 1씩 더해 층 이름을 “conv_i”로 합니다. ReLU, 풀링, 배치 정규화도 마찬가지로 조건문에 따라 이름을 만듭니다. 그리고 VGG19 에서 추출한 층을 우리가 정의한 model 에 추가해 줍니다(model.add_module(name, layer)).

if name in content_layers: VGG19 에서 추출한 layer 중에서 우리가 정의한 content_layers 와 동일한 이름의 layer 가 있다면 해당 층의 내용 손실 함수에 대해 정의하고 모델에 추가합니다.

if name in style_layers: 마찬가지로 VGG19 에서 추출한 layer 중에서 style_layers 에 속하면 스타일 손실 함수에 대해 정의하고 모델에 추가합니다.

for i in range(len(model) - 1, -1, -1): 두 번째 루프문은 우리가 구성한 model 을 역순으로 읽어 최종 손실 함수가 있는 위치를 파악합니다. 최종 손실 함수가 있는 부분만 사용하므로 i 번째까지 층을 잘라 그 뒤는 배제한 모델로 재정의 합니다.

# 모델 재구성 및 손실 레이어 주입
def get_style_model_and_losses(cnn, style_img, content_img):

    """
    사전 학습된 cnn(e.g., VGG19.features)를 기반으로 ContentLoss와 StyleLoss 모듈이
    '주입된' 새로운 nn.Sequential 모델을 만듭니다.

    Args:
        cnn: VGG.features와 같이 nn.Conv2d, nn.ReLU 등으로 구성된 모델
        style_img: (1, 3, 256, 256) 크기의 원본 스타일 이미지
        content_img: (1, 3, 256, 256) 크기의 원본 내용 이미지
    """

    # 손실을 계산할 VGG 레이어 이름 지정
    content_layers = ['conv_4']
    style_layers = ['conv_1', 'conv_2', 'conv_3', 'conv_4', 'conv_5']

    # ImageNet 정규화 값
    normalization_mean = torch.tensor([0.485, 0.456, 0.406]).to(device)
    normalization_std = torch.tensor([0.229, 0.224, 0.225]).to(device)

    # 정규화 모듈 생성
    normalization = Normalization(normalization_mean, normalization_std).to(device)

    # 손실 모듈을 담을 리스트
    content_losses = []
    style_losses = []

    # 새로운 nn.Sequential 모델 생성.
    # 첫 번째 레이어는 '정규화' 레이어입니다.
    model = nn.Sequential(normalization)

    i = 0 # conv 레이어 카운터
    for layer in cnn.children():

        # 원본 cnn 의 각 레이어를 순회
        if isinstance(layer, nn.Conv2d):
            i += 1
            name = 'conv_{}'.format(i)
        elif isinstance(layer, nn.ReLU):
            name = 'relu_{}'.format(i)

            # 중요: 원본 VGG가 'inplace=True'로 ReLU 를 사용할 수 있습니다. 하지만 우리는 ReLU 의 출력을 받아 손실을 계산해야 하므로,
            # inplace 연산이 다음 레이어에 영향을 주는 것을 막기 위해 'inplace=False' 로 강제로 새 ReLU 를 만듭니다.
            layer = nn.ReLU(inplace=False)
        elif isinstance(layer, nn.MaxPool2d):
            name = 'maxpool_{}'.format(i)
        elif isinstance(layer, nn.BatchNorm2d):
            name = 'bn_{}'.format(i)
        else:
            raise RuntimeError('Unrecognized layer: {}'.format(layer.__class__.__name__))

        # 새 model 에 VGG 레이어를 순서대로 추가
        model.add_module(name, layer)

        # Content Loss 주입
        if name in content_layers: 
            # 원본 '내용' 이미지를 '현재까지 만들어진 모델'에 통과시켜 해당 레이어의 특징 맵(target)을 추출합니다.
            target = model(content_img)
            # ContentLoss 모듈을 생성
            content_loss = ContentLoss(target)
            # 'conv_4' 바로 뒤에 'content_loss_4' 모듈을 추가
            model.add_module("content_loss_{}".format(i), content_loss)
            content_losses.append(content_loss)

        # Style Loss 주입
        if name in style_layers: 
            # 원본 '스타일' 이미지를 '현재까지 만들어진 모델'에 통과시켜 해당 레이어의 특징 맵을 추출합니다.
            target_feature = model(style_img)

            # StyleLoss 모듈을 생성
            style_loss = StyleLoss(target_feature)

            # 해당 레이어 바로 뒤에 'style_loss_i' 모듈을 추가
            model.add_module("style_loss_{}".format(i), style_loss)
            style_losses.append(style_loss)
    # 모델 자르기
    # content/style 손실에 필요한 마지막 레이어 뒤쪽은 필요 없습니다. (e.g, VGG의 classifier 부분)
    # 뒤에서부터 순회하며 마지막 loss 모듈을 찾습니다.
    for i in range(len(model) - 1, -1, -1): 
        if isinstance(model[i], ContentLoss) or isinstance(model[i], StyleLoss):
            break

    # 모델을 [첫 레이어 : 마지막 loss 모듈]까지 잘라냅니다.
    model = model[:(i + 1)] 

    return model, style_losses, content_losses

결과 이미지 최적화 하기

앞서 정의한 get_style_model_and_losses 을 이용해 특정 층에 손실 함수가 들어있는 모델을 만들고 손실 함수와 함께 정의합니다.

최적화 기법으로는 L-BFGS(Limited-memory-Broyden-Fletcher-Goldfarb-Shanno algorithm) 를 사용하며 우리는 모델 최적화가 아닌 입력 이미지를 최적화하는 것이므로 변수에 [input_img] 을 넣어줍니다. LBFGS 는 헤시안 행렬(2차 미분)을 계산하는 방법으로 closure() 를 정의하여 1차 미분값들을 저장해야 합니다. 그리고 LBFGS 와 같은 최적화 함수들은 추후에 따로 한 번 정리를 할건데 그 때 상세히 다루도록 하겠습니다.

학습 과정은 closure() 함수 내에서 진행하게 합니다.

input_img.data.clamp_(0, 1) 이미지 값을 0 이상 1 이하에서 관리하기 위해 clamp 함수를 사용합니다. clamp_(0,1) 는 input_img 의 값을 0과 1 기준으로 절삭하여 0 이상 1 이하의 값만 사용하도록 합니다. 또한 _ 는 in-place 방식이라는 의미로 별도의 = 없이 원래 input_img 값을 절삭한 input_img 로 만듭니다.

# 스타일 트랜스퍼 실행
def run_style_transfer(cnn, content_img, style_img, num_steps=300, style_weight=100000, content_weight=1):
    
    # 1. 최적화 대상 이미지 설정
    # '내용' 이미지를 복제하여 '생성할 이미지(input_img)'의 시작점으로 삼습니다.
    # requries_grad_(True) 설정이 핵심입니다.
    # 이 모델은 '네트워크의 가중치'를 학습하는 것이 아니라, '입력 이미지(input_img)의 픽셀' 자체를 학습(최적화)합니다.
    input_img = content_img.clone().detach().requires_grad_(True)

    # 2. 모델 및 손실 함수 준비
    # 위에서 정의한 함수로 VGG를 재구성한 모델과 손실 모듈 리스트(style_losses, content_losses)를 가져옵니다.
    model, style_losses, content_losses = get_style_model_and_losses(cnn, style_img, content_img)

    # 3. 옵티마이저 설정
    # 최적화할 대상은 '모델 가중치가'가 아닌 [input_img] 입니다.
    # LBFGS 는 이 작업에 Adam 이나 SGD 보다 효율적인 경향이 있습니다.
    optimizer = optim.LBFGS([input_img])
    iteration = [0]
    while iteration[0] <= num_steps:

        # LBFGS 옵티마이저는 'closure' 라는 함수를 optimizer.step()에 전달해야 합니다.
        # 이 함수는 1. 그래디언트 초기화, 2. 손실 계산, 3. 손실 반환을 수행합니다.
        def closure():

            # 픽셀 값이 0~1 범위를 벗어나지 않도록 고정(clamp)
            input_img.data.clamp_(0, 1) 
            optimizer.zero_grad()

            # 생성 중인 이미지(input_img)를 재구성된 모델에 통과시킵니다.
            # 이 과정에서 input_img가 각 손실 모듈(ContentLoss, StyleLoss)을 지날 때마다, 해당 모듈 내의 'self.loss' 값이
            # '부수 효과(side-effect)'로 계산되고 업데이트 됩니다.
            model(input_img) 

            # 각 손실 모듈에 저장된 'self.loss' 값을 모두 더합니다.
            style_score = 0
            content_score = 0

            for sl in style_losses:
                style_score += sl.loss 
            for cl in content_losses:
                content_score += cl.loss 

            # 가중치를 적용한 최종 손실 계산
            loss = style_weight*style_score + content_weight*content_score 

            # 손실(loss)에 대해 'input_img'의 픽셀에 대한 그래디언트를 계산합니다.
            loss.backward()

            # 반복 횟수 증가 (closure 내부에서 외부 변수 변경 위해 리스트 사용)
            iteration[0] += 1
            if iteration[0] % 50 == 0:
                print('Iteration {}: Style Loss : {:4f} Content Loss: {:4f}'.format(
                    iteration[0], style_score.item(), content_score.item()))

            # LBFGS 는 이 반환된 loss 를 사용합니다.
            return style_score + content_score

        # 옵티마이저가 closure 를 실행하고, 계산된 그래디언트(loss.backward())를 사용해 input_img 의 픽셀을 업데이트합니다.
        optimizer.step(closure)

    # 최정 생성된 이미지의 픽셀 값을 0~1 사이의 값으로 고정하여 반환
    return input_img.data.clamp_(0, 1)

예제 이미지 불러오기

image_loader 를 통해 이미지 사이즈는 256x256 으로 설정하고 4채널 이미지에 대해 3채널로 변경하기 위해 이미지를 불러온뒤 .convert(‘RGB’) 를 적용합니다.

def image_loader(img_path):
    loader = transforms.Compose([transforms.Resize((256, 256)), transforms.ToTensor()])
    image = Image.open(img_path).convert('RGB')
    image = loader(image).unsqueeze(0) # 4차원 텐서 변환
    return image.to(device)

style_img = image_loader("/content/drive/MyDrive/pytorch/data/imgA.jpg")
content_img = image_loader("/content/drive/MyDrive/pytorch/data/imgB.jpg")

이미지 학습하기

output = run_style_transfer(cnn, content_img, style_img)

Output: 

Iteration 50: Style Loss : 0.000169 Content Loss: 50.467072
Iteration 100: Style Loss : 0.000041 Content Loss: 38.233650
Iteration 150: Style Loss : 0.000028 Content Loss: 32.563766
Iteration 200: Style Loss : 0.000022 Content Loss: 29.903051
Iteration 250: Style Loss : 0.000019 Content Loss: 28.473398
Iteration 300: Style Loss : 0.000018 Content Loss: 27.525640

결과 이미지 보기

style_image 와 input_image 는 다음과 같습니다.

output_image 는 input_image 에 style_image 를 입힌 것입니다. 결과는 다음과 같습니다.

7. 깊은 K-평균 알고리즘

이번엔 앞에서 배운 오토인코더와 K-평균 알고리즘을 조합하여 이미지를 클러스터링해 보도록 하겠습니다. 데이터는 MNIST 데이터를 사용하며 훈련 데이터에 라벨이 없다고 가정하고 비지도 학습으로 모델을 학습합니다. 오토인코더는 인코더 부분에 이미지가 들어와서 차원이 축소된 잠재 변수를 생성한 뒤 다시 디코더를 거쳐 원래 이미지와 같은 크기의 이미지를 출력합니다.
즉, 잠재 변수와 크기가 같은 적절한 벡터를 디코더 부분에 주입하게 되면 가상 이미지가 생성되고 잠재 변수는 실제 이미지를 압축한 벡터로써 이미지에 대한 중요한 정보를 담고 있다고 볼 수 있습니다. 따라서 잠재 변수를 활용하여 이미지를 분류한다면 좋은 결과를 얻을 수 있을 것이며, 이를 깊은 K-평균 알고리즘(Deep K-Means)라고 합니다.

이 모델의 손실 함수는 $ L = L_{r} + \lambda L_{c} $ 로 정의합니다. 여기서 $L_{r}$ 은 오토인코더의 이미지 재구성(reconstruction) 부분을 담당하며 $L_{c}$ 는 클러스터링의 최적 중심과 잠재 변수 간의 거리를 측정하는 것으로 정의합니다.
좀 더 상세히 알아보자면 오토인코더의 손실 함수는 MSE(평균 제곱 오차)를 사용하며 구체적으로 $L_r = \sum_{i=1}^{N} | x_i - g_\phi(f_\theta(x_i)) |^2$ 로 정의할 수 있습니다.
군집화 손실 함수는 K-Means 의 목표는 각 데이터 포인트와 가장 가까운 군집 중심 간의 거리 제곱의 합을 최소화하는 것입니다. 이를 수식으로 나타내면 $L_c = \sum_{i=1}^{N} \min_{j \in {1, \dots, K}} | f_\theta(x_i) - \mu_j |^2$ 이며 두 수식을 결합하면 아래와 같이 정의할 수 있습니다.

\[L(\theta, \phi, \{\mu_j\}_{j=1}^K) = \sum_{i=1}^{N} \| x_i - g_\phi(f_\theta(x_i)) \|^2 + \lambda \sum_{i=1}^{N} \min_{j \in \{1, \dots, K\}} \| f_\theta(x_i) - \mu_j \|^2\]

기본적으로 좋은 잠재 변수가 추출되려면 이미지 생성을 잘해야만 합니다. 따라서 클러스터링 부분보다는 오토인코더 부분에 더 비중을 주기 위해 $\lambda$ 에 작은 값을 주어 학습을 조율합니다.

각 구성 요소의 상세 설명은 다음과 같습니다

• $N$ : 전체 데이터 샘플의 수
• $x_i$ : $i$번째 원본 데이터 샘플 (고차원)
• $f_\theta(\cdot)$ : 인코더(Encoder) 네트워크. 파라미터 $\theta$를 가짐.
• $z_i = f_\theta(x_i)$ : $x_i$가 인코더를 통과한 잠재 벡터 (저차원)
• $g_\phi(\cdot)$ : 디코더(Decoder) 네트워크. 파라미터 $\phi$를 가짐.
• $\hat{x}i = g\phi(z_i)$ : 잠재 벡터 $z_i$로부터 복원된 데이터 샘플
• $K$ : 군집의 수
• $\mu_j$ : $j$번째 군집의 중심(centroid) 벡터. 잠재 공간 $z$와 동일한 차원을 가짐.

7.2 모델 코드 설명

라이브러리 불러오기

import torch
import torch.nn as nn
import torchvision
from torchvision import transforms
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import linear_sum_assignment as linear_assignment
from sklearn.manifold import TSNE

데이터 불러오기

MNIST 데이터를 불러오며, 배치 사이즈, 클러스터 개수, 잠재 변수의 크기를 정합니다.

batch_size = 128
num_clusters = 10
latent_size = 10

trainset = torchvision.datasets.MNIST("./data/", download=True, train=True, transform=transforms.ToTensor())
testset = torchvision.datasets.MNIST("./data/", download=True, train=False, transform=transforms.ToTensor())

trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size, shuffle=True)
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size, shuffle=True)

벡터화, 피쳐맵화 클래스 정의하기

이전에 배웠던 합성곱 오토인코더를 사용합니다. 따라서 그에 맞게 잠재 변수의 벡터를 변형시키는 Flatten, Deflatten 클래스를 정의합니다.

# 인코더의 출력 결과인 특징 맵을 일렬 벡터로 만들어주는 클래스
class Flatten(torch.nn.Module):
  def forward(self, x):
    batch_size = x.shape[0]
    return x.view(batch_size, -1)

# 일렬 벡터를 디코더의 입력에 사용하기 위해 다시 특징 맵으로 바꿔주는 클래스
class Deflatten(nn.Module):
  def __init__(self, k):
    super(Deflatten, self).__init__()
    self.k = k

  def forward(self, x):
    s = x.size()
    feature_size = int((s[1]//self.k)**0.5)
    return x.view(s[0], self.k, feature_size, feature_size)

K-평균 알고리즘 정의하기

centroids 는 최적화가 되어야 할 변수이므로, nn.Parameter 로 정의합니다. 그리고 처음엔 임의의 값으로 중심 값을 초기화 합니다.

argminl2distance 함수는 잠재 변수의 그룹화를 위해 가장 가까운 중심을 argmin 함수로 찾습니다. 즉, torch.sum((a-b)**2, dim=1) 은 잠재 변수와 각 중심과의 유클리드 거리를 측정한 것이고, torch.argmin(torch.sum((a-b)**2, dim=1), dim=0) 은 각 거리들 중 가장 가까운 중심의 인덱스를 추출하는 것입니다.

중심인 centroids 와 잠재 변수 간의 군집을 진행합니다.

class Kmeans(nn.Module):
  def __init__(self, num_clusters, latent_size):
    super(Kmeans, self).__init__()
    self.num_clusters = num_clusters

    # 클러스터 개수 만큼 임의의 값을 가지는 중심점 생성
    self.centroids = nn.Parameter(torch.rand((self.num_clusters, latent_size)).to(device))

  def argminl2distance(self, a, b):
    return torch.argmin(torch.sum((a-b)**2, dim=1), dim=0)

  def forward(self, x):
    y_assign = []
    for m in range(x.size(0)):
      h = x[m].expand(self.num_clusters, -1)
      assign = self.argminl2distance(h, self.centroids)
      y_assign.append(assign.item())
    
    # 각 입력 값들이 중심점과 연관성이 높은 곳으로 모은 리스트와, 중심점을 반환
    return y_assign, self.centroids[y_assign]

오토인코더 정의하기

이전에 배웠던 합성곱 오토인코더를 그대로 사용합니다.

# 합성곱 오토인코더의 인코더
class Encoder(nn.Module):
  def __init__(self, latent_size):
    super(Encoder, self).__init__()

    k = 16
    self.encoder = nn.Sequential(
        nn.Conv2d(1, k, 3, stride=2),
        nn.ReLU(),
        nn.Conv2d(k, 2*k, 3, stride=2),
        nn.ReLU(),
        nn.Conv2d(2*k, 4*k, 3, stride=1),
        nn.ReLU(),
        Flatten(),
        nn.Linear(1024, latent_size),
        nn.ReLU())

  def forward(self, x):
    return self.encoder(x)

# 합성곱 오토인코더의 디코더
class Decoder(nn.Module):
  def __init__(self, latent_size):
    super(Decoder, self).__init__()
    k = 16
    self.decoder = nn.Sequential(
        nn.Linear(latent_size, 1024),
        nn.ReLU(),
        Deflatten(4*k),
        nn.ConvTranspose2d(4*k, 2*k, 3, stride=1),
        nn.ReLU(),
        nn.ConvTranspose2d(2*k, k, 3, stride=2),
        nn.ReLU(),
        nn.ConvTranspose2d(k, 1, 3, stride=2, output_padding=1),
        nn.Sigmoid())

  def forward(self, x):
    return self.decoder(x)

클러스터 평가 함수 정의하기

평가를 위해 실제 라벨과 예측 라벨을 파라메터로 받아옵니다.

클러스터 평가를 위해 라벨 수 x 라벨 수 행렬을 만듭니다. 그리고 열과 행 중 실제 라벨과 예측 라벨을 정의하고, 정의한 대로 행렬에 1을 누적시킵니다.

누적과정이 끝나면 실제 라벨과 예측 라벨이 같은 것들의 수에서 전체 라벨 수를 나누어 정확도를 계산합니다.

def cluster_acc(y_true, y_pred):
    """
    K-Means 와 같은 비지도 클러스터링의 정확도를 계산합니다.
    클러스터 할당(y_pred)와 실제 레이블(y_true) 간의 최적의 매핑을 찾아 정확도를 계산합니다.
    """

    """
    Args:
        y_true : 실제 정답 레이블
        y_pred : 모델이 예측한 클러스터 번호
    """

    # 입력을 numpy array 로 변환
    y_true = np.array(y_true)
    y_pred = np.array(y_pred)

    # 클래스/클러스터의 개수 확인
    # MNIST 데이터의 경우 10개
    D = max(y_pred.max(), y_true.max()) + 1

    # 혼동 행렬(Confusion Matrix) 또는 비용 행렬(Cost Matrix) 생성
    # w[i, j] = "예측 클러스터가 i"이고 "실제 레이블이 j인 샘플의 개수"
    w = np.zeros((D, D), dtype=np.int64)
    for i in range(y_pred.size):
        w[y_pred[i], y_true[i]] += 1
    
    # 예시: w[0, 7] = 500
    # 클러스터 0으로 예측된 것 중에 실제 레이블이 7인 것이 500개라는 의미

    # 최적의 매핑 찾기
    # linear_assignment 함수는 '비용(cost)'을 '최소화'하는 매칭을 찾습니다.
    # 우리는 '일치하는 샘플 수(w)' 를 '최대화'하고 싶습니다.
    # 따라서 (최대값 - w)를 비용 행렬로 사용하여 최소화 문제를 풉니다.
    # 가장 많이 일치하는 w[i, j] 값이 가장 작은 비용이 됩니다.
    cost_matrix = w.max() - w
    row_ind, col_ind = linear_assignment(cost_matrix)

    # (결과 예시: row_ind=[0, 1, 2], col_ind=[7, 3, 0])
    # -> 클러스터 0은 레이블 7에,
    # -> 클러스터 1은 레이블 3에,
    # -> 클러스터 2는 레이블 0에 매핑하는 것이 최적이라는 의미.

    correct_count = sum([w[i, j] for i, j in zip(row_ind, col_ind)])
    return correct_count * 1.0 / y_pred.size

def evaluation(testloader, encoder, kmeans, device):
  predictions = []
  actual = []

  with torch.no_grad():
    for images, labels in testloader:
      inputs = images.to(device)
      labels = labels.to(device)
      latent_var = encoder(inputs)
      y_pred, _ = kmeans(latent_var)

      predictions += y_pred
      actual += labels.cpu().tolist()
    
  return cluster_acc(actual, predictions)

손실 함수 및 최적화 방법 정의하기

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
encoder = Encoder(latent_size).to(device)
decoder = Decoder(latent_size).to(device)
kmeans = Kmeans(num_clusters, latent_size).to(device)
criterion1 = torch.nn.MSELoss()
criterion2 = torch.nn.MSELoss()
optimizer = torch.optim.Adam(list(encoder.parameters()) + list(decoder.parameters()) + list(kmeans.parameters()), lr=1e-3)

모델 학습 변수 설정하기

앞서 설명했듯이 Deep K-Means 모델은 $\lambda$ 에 민감합니다. 따라서 학습 초반에는 작은 값으로 시작해서 학습 횟수에 따라 점차 값을 증가 시키는 방식으로 모델을 학습합니다. 따라서 이에 따라 $\lambda$ 에 대한 기준을 정합니다.

T1 = 50
T2 = 200
lam = 1e-3
ls = 0.05

모델 학습 하기

for epoch in range(300):
  if (epoch > T1) and (epoch < T2):
    alpha = lam *(epoch-T1) / (T2-T1)
  elif epoch >= T2:
    alpha = lam
  else:
    alpha = lam/(T2-T1)
  
  running_loss = 0.0
  for images, _ in trainloader:
    inputs = images.to(device)
    optimizer.zero_grad()
    latent_var = encoder(inputs)
    _, centroids = kmeans(latent_var.detach())
    outputs = decoder(latent_var)

    l_rec = criterion1(inputs, outputs)
    l_clt = criterion2(latent_var, centroids)
    loss = l_rec + alpha*l_clt
    loss.backward()
    optimizer.step()
    running_loss += loss.item()
  avg_loss = running_loss / len(trainloader)

  if epoch % 10 == 0:
    testacc = evaluation(testloader, encoder, kmeans, device)
    print('[%d] Train loss: %.4f, Test Accuracy: %.3f' %(epoch, avg_loss, testacc))
  
  if avg_loss < ls:
    ls = avg_loss
    torch.save(encoder.state_dict(), "/content/drive/MyDrive/pytorch/models/dkm_en.pth")
    torch.save(decoder.state_dict(), "/content/drive/MyDrive/pytorch/models/dkm_de.pth")
    torch.save(kmeans.state_dict(), "/content/drive/MyDrive/pytorch/models/dkm_clt.pth")

Output: 
[0] Train loss: 0.0169, Test Accuracy: 0.801
[10] Train loss: 0.0169, Test Accuracy: 0.804
[20] Train loss: 0.0169, Test Accuracy: 0.805
[30] Train loss: 0.0169, Test Accuracy: 0.803
[40] Train loss: 0.0169, Test Accuracy: 0.802
... 생략 ...

최종 모델 평가하기

predictions = []
actual = []
latent_features = []
with torch.no_grad():
    for images, labels in testloader: 
        inputs = images.to(device)
        labels = labels.to(device)
        latent_var = encoder(inputs)
        y_pred, _ = kmeans(latent_var)
        
        predictions += y_pred
        latent_features += latent_var.cpu().tolist()
        actual += labels.cpu().tolist()
            
print(cluster_acc(actual, predictions))

Output: 0.8

실제 이미지와 생성된 이미지 비교

with torch.no_grad():
    for images, _ in testloader: 
        inputs = images.to(device)
        latent_var = encoder(inputs)
        outputs = decoder(latent_var)
        
        input_samples = inputs.permute(0,2,3,1).cpu().numpy()
        reconstructed_samples = outputs.permute(0,2,3,1).cpu().numpy()
        break

columns = 10
rows = 5
print("Input images")  
fig=plt.figure(figsize=(columns, rows))
for i in range(1, columns*rows+1):
    img = input_samples[i-1]
    fig.add_subplot(rows, columns, i)
    plt.imshow(img.squeeze())
    plt.axis('off')
plt.show()

print("Reconstruction images") 
fig=plt.figure(figsize=(columns, rows))
for i in range(1, columns*rows+1):
    img = reconstructed_samples[i-1]
    fig.add_subplot(rows, columns, i)
    plt.imshow(img.squeeze())
    plt.axis('off')  
plt.show()

군집 결과 시각화

tsne = TSNE(n_components=2, random_state=0)
cluster = np.array(tsne.fit_transform(np.array(latent_features)))
actual = np.array(actual)

plt.figure(figsize=(10, 10))
mnist = range(10)
for i, label in zip(range(10), mnist):
    idx = np.where(actual == i)
    plt.scatter(cluster[idx, 0], cluster[idx, 1], marker='.', label=str(label))
plt.legend()
plt.show()

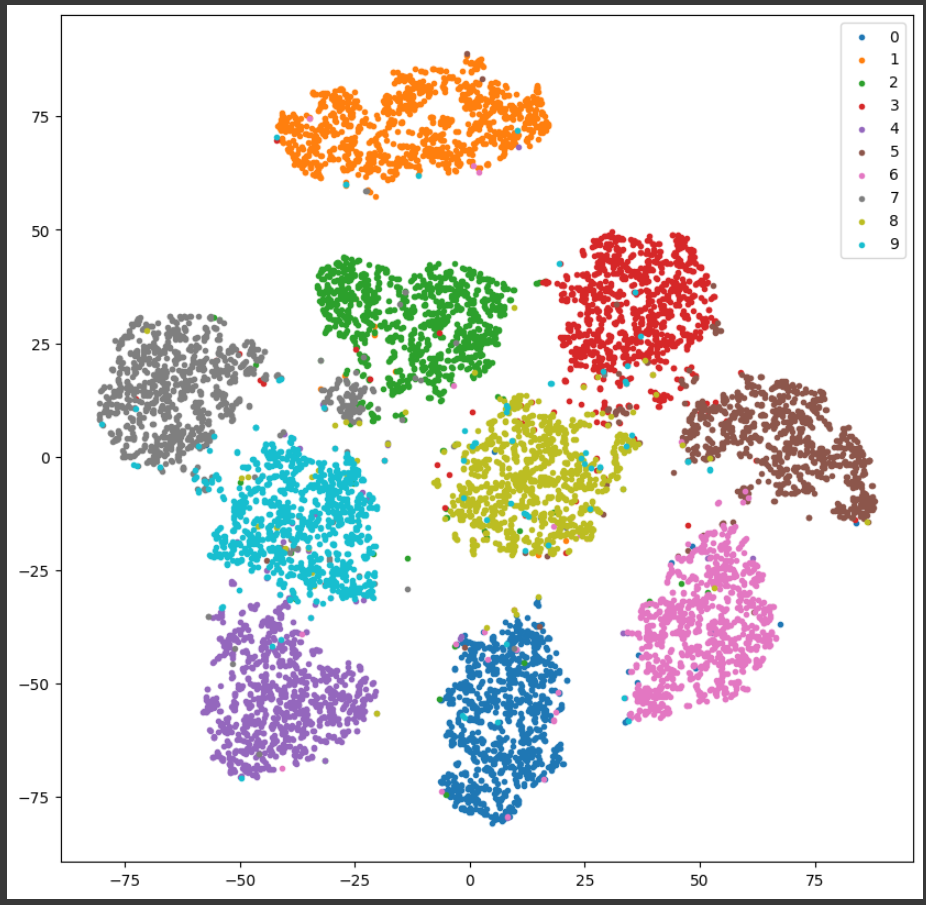
마치며

최근 LLM 모델들이 연신 최고 성능을 뽐내고 있습니다. LLM 도 사전 학습은 라벨이 없는 데이터를 이용한 Language Model 이기 때문에 이번에 파이토치를 이용한 비지도 학습에 대한 포스트를 정리하면서 LLM 에 사용된 비지도 학습에 대해서 자세히 알 수 있었고, 대략적으로 알던 비지도 학습에 대한 개념들도 확실히 정리하고, 구체적인 예제들도 직접 진행해 굉장히 건설적인 시간이었습니다.